立体匹配中的全局匹配（一）动态规划笔记
近来研究立体匹配，从入门开始，先学习1些基本的算法思想。
立体匹配算法中，全局匹配是1个很重要的部份，利用图象的全局束缚信息，对局部图象的模糊不敏感，它的计算代价很高。全局匹配算法通过构建全局能量函数，然后通过优化方法最小化全局能量函数以求得致密视差图。
全局匹配算法1般有动态计划、置信传播、摹拟退火、图割法、遗传学等，这里首先介绍动态计划，也是从1些论文中提取的思想，可能有不对的地方，望指正。
动态计划的思想就是把求解全部图象深度值的进程分解为1些子进程，逐一求解子进程，具体进程为根据外极线顺序束缚，通过在视差图象上寻觅最小代价路径得到终究视差图，从而减少了算法的复杂度，动态计划的思想体现了顺序束缚和连续性束缚。传统的动态计划算法可以很好的处理因局部纹理单1而酿成的误匹配，算法复杂度不高，缺点是匹配进程疏忽了每条极线间视差的束缚，致使了视差图有条纹瑕疵现象。
参考论文：
双目视觉立体匹配方法研究-魏朋玉-重庆大学
基于动态计划的立体匹配算法研究-龚文-南昌航空大学
基于动态计划和置信传播 的立体匹配算法的研究 -刘英杰-燕山东大学学
1：首先了解下动态计划算法的思想：
解决爬楼梯的问题：
1个人每次只能走1层楼梯或两层楼梯，问走到80层1共有多少种方法。
解：设DP[i]为走到第i层1共有多少种方法，那末DP[80]就是所求的目标。很明显DP[1]=1,DP[2]=2(走到第1层只有1种就是走1层楼梯，第2层有两种：走两次1层楼梯或走1次两层楼梯)。同理走到第[i]层楼梯可以从第i⑴层走1层，或从i⑵走两层。很容易得到：
递推公式：DP[i]=DP[i⑴]+DP[i⑵]
边界条件：DP[1]=1 DP[2]=2
则自顶向下的解法：
long long dp[81] = {0};/*用于保存中间结果
否则会重复计算很多重复的子问题*/
long long DP(int n)
{
if(dp[n])
return dp[n];
if(n == 1)
return 1;
if(n == 2)
return 2;
dp[n] = DP(n-1) + DP(n-2);
return dp[n];
} 自低向上的解法：
int i;
long long dp[81]; /* 注意当n超过75时，结果值将超过int范围 */
dp[1] = 1;
dp[2] = 2;
for(i=3; i <= 80; i++)
dp[i] = dp[i-1] + dp[i-2]; 动态计划大致就是这个思路。
2：动态计划立体匹配基于极线束缚，通过顺次寻觅每条极线上匹配点对的最小代价路径的动态寻优方法求解全局能量最小化，得到匹配视差图。算法步骤：
A：阶段划分：传统的方法是只在水平方向寻觅扫描点，所以算法是在水平扫描线的视差空间切面上寻觅最优路径的进程，以像素点的行方向为横坐标，视差值d为纵坐标，顺次将全部进程分为1,2,3,4……k个阶段，每一个x坐标点对应1个阶段，把立体匹配划分成可以排序的若干个阶段。
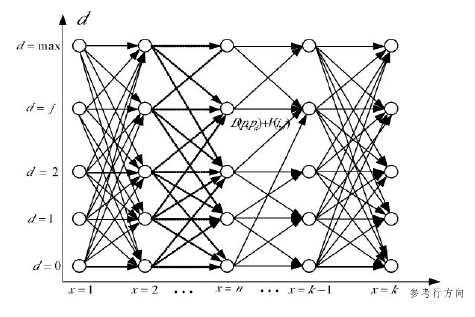
B：肯定状态
将上述各个阶段所处的匹配阶段用不同的状态表示。状态的选择要满足无后向性。无后向性的意思就是当前阶段的状态只是之前阶段的综合结果，其实不对后续阶段产生影响。
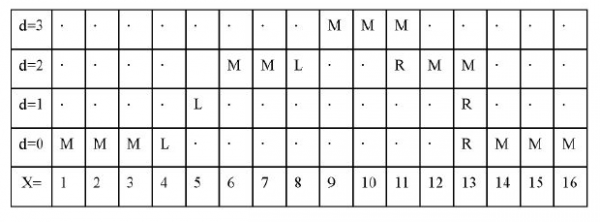
共有3种状态：相互匹配M，左可见右遮挡为L（某点在右图中没有匹配点），右可见左遮挡为R（如果前1个点的视差比后1个视差大，就是前面点的匹配点在后1个点的匹配点的后面）。
C：状态转移方程：所谓状态转移方程就是根据前1阶段的状态肯定当前阶段的状态，根据顺序性的束缚，允许的状态转移情势有7种（用小写字母表示前1阶段的状态，大写字母表示当前阶段的状态）
0表示正确匹配，1、2表示匹配产生左图象遮挡，4、5表示产生右图象遮挡点，3、6表示图象由背景进入前景，视差跳变产生其实不连续点。
D：求取最优解，并记录该最优解的路径
在实际编程中，按顺序自左向右，或自右向左对各阶段（即同1极线上的点）顺次进行计算，计算类似性测度函数和平滑函数的最小值，当所有阶段都计算完成后，全局能量函数最小的1条最优匹配路径也就得出来了。
全局能量函数表示以下，
E(d)= E(data) + E(smooth)
其中 E(data) 为图象数据束缚项，判断匹配像素点之间的类似性， E(smooth)为相邻点间的平滑束缚项，判断相邻点之间的连续性。
数据项由匹配代价取得
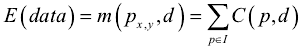
其中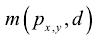
表示左像素点与视差为d的右像素点的匹配代价函数。
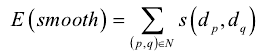
其中N表示相邻像素对的集合，dp，dq分别表示像素点p与像素点q的视差，平滑项s(dp,dq)表示相邻像素点p、q之间的平滑束缚，定义以下：
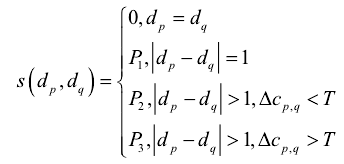
其中P1，P2，P3表示不同情况下的惩罚常量，Cp,q表示待匹配的像素点与其相邻点q之间的色采差异，当相邻点视差值相同时，惩罚量为0;差值为1时惩罚量为P1，当差值大于1且两个对应像素点的色采差异小于阈值T时，惩罚量为P2，否则惩罚量为P3。P1，P2，P3，T分别赋值10、20、40、35 。
Cp,q也能够是图象中相邻像素点p和q之间的梯度。
最优解d*=arg minE(d)，这里是指使E(d)获得最小值时的d值。d是1个数组，传统的是1行行求每一个点的视差，每行组合起来就是视差图，并且是稠密的。
传统的动态计划思想：
我做1个类比，求这个最优路径就相当于上面求怎样最少步数的登上80层，每步上几个台阶就相当于每个点的视差值，每点的视差值得范围是设定的视差搜索范围，求出最优路径就是把每步上的台阶数计算出来了，相当于每步的视差也就计算出来了。边界值就设为0，可能有更好的想法，然后顺次计算。
先逐一计算每一个像素在每一个视差下的匹配代价聚合值，这样1行像素就构成1个以行像素为横坐标，以视差值为纵坐标的2维数组，然后根据唯1性束缚温柔序性束缚使全局能量函数最小，就是求所有点的视差匹配代价加上平滑束缚得到的值最小。这样既求得比较精确的视差又让视差平滑了。
不知道这样理解对不对。谁理解的更好，请指点1下，菜鸟求指点
这样的动态计划求出的只是在水平扫描线上寻径，疏忽了扫描线间视差的束缚，视差图有明显的条纹现象。
3：改进的动态计划：
A：基于行列双通道的动态计划算法，在行扫描线上寻径的同时斟酌垂直方向的视差1致束缚，对扫描行间也进行动态计划的寻优。首先用水平路径所求的匹配视差结果作为初始视差值，再次在列方向上2次动态寻优，求取能量函数最小值，生成致密视差图。
引入1种赏罚的方法，通过减小初始视差值d*所对应匹配代价函数的值来引导其在列方向动态寻优，行将在行方向上动态寻优求解得到的初始视差值作为1个结果，然后对这个视差结果对应的数据项给予1个更新，其它数据项在这个进程中保持不变。
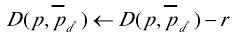
r是1个相对代价函数较小的数，这里取3，太大会对列寻优没作用，太小对行寻优没意思。
在列方向上进行动态寻优，即为只斟酌列方向上相邻像素点的视差束缚，运算进程与行方向1致。这样可以改啥条纹现象，但时间复杂度比原来高出1倍，失去了效力优势。
这样得到的结果有少许明显的视差点。后处理方法：在行方向上如果1个像素点左右邻域上像素点的视差相等，则把其左右邻域像素视差值赋予该像素点；在列方向上如果1个像素点其上下邻域像素点的视差相等，则将其上下邻域像素的视差值赋予该像素点，其它情况下不变。
B：基于树结构的动态计划算法
在全局能量函数中的平滑项 E(smooth)表示相邻像素点p、q在其对应视差值dp、dq情况下束缚项。
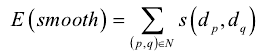
其中集合N表示像素点间相互束缚的邻域范围，这个算法是研究邻域N的几种树结构DP算法。
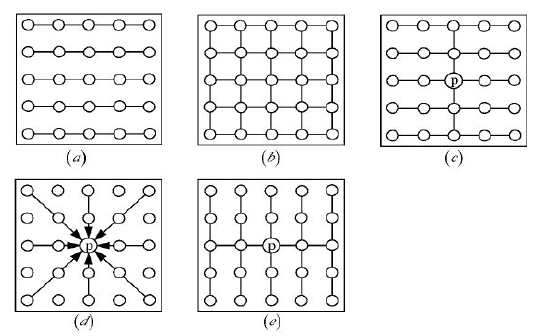
a就是传统的行扫描线动态寻优；
b是1种类似于树的结构来连接4个方向的点，排除边界点与角点，邻域N选择上下左右4个方向，每一个点都与它的4个相邻像素点有关，算法有效解决行扫描线间的垂直束缚问题。
c、e是算法对每个像素点建立水平和垂直两个方向的树结构，首先在行扫描方向进行动态寻优计算最好匹配代价值，然后检查最优值是否是也是垂直方向的最优值，用WTA得到最优视差值。
d是将匹配中2维束缚近似转化为多个1维束缚，采取以中心像素点为根节点的8个不同方向的平滑束缚对图象进行动态计划寻径，缺点是在求解最优视差值的进程中各个方向都不能提供有效的纹理信息使得算法在弱纹理区域误匹配率高。
其中b的解决方案：
首先对每列做向下的动态计划运算，得到极线间从最左侧开始的每个像素的最优匹配代价，将所得的优化代价寄存在矩阵
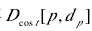
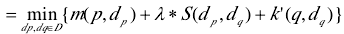
接着对每列做向上的动态计划运算，得到极线间从最下边开始的每个像素的左右匹配代价，这时候的q指向p下面的像素，把得到的结果寄存在矩阵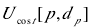
为了得到每一个像素的优化代价，可以将向上和向下动态计划运算代价进行积累，在座标（x,y）的像素记为px,y，则赋予它视差d时的最小能量函数
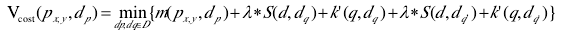
上式等于
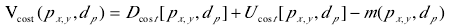
最后在得到优化矩阵后，将极线间的动态计划与极线上的动态计划结合，用已获得的运算结果更新视差空间代价值
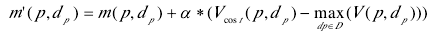
其中a是用来调剂极线间动态计划对视差结果影响的参数。
然落后行极线上的动态计划，在基于上面的更新后的视差空间进行的，最后把积累结果寄存在矩阵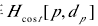
最小化这个矩阵，就能够求取每一个像素的视差了。
这类方法复杂度过大，时间太长。
4：基于控制点的双向动态计划匹配。
利用事前肯定的正确匹配点作为匹配控制点，在动态计划进程中对寻优路径进行指点，从而煎炒条纹瑕疵，下降了复杂度。
控制点是那些事前知道的正确的匹配点。那末就能够通过将这些正确匹配点设为1个较小值迫使所找寻的路径经过这些正确点。这些点满足左右1致性束缚；避免伪最优匹配，匹配代价小于遮挡代价，排除孤立的控制点，即那些没有直接近邻控制点的点。
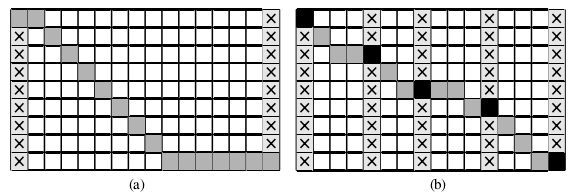
b中的斑点就是控制点，有效缩小搜索空间。
具体步骤：
A：得到每一个像素的初始匹配代价C(x,y,d)，处理遮挡问题需要计算出左右视差图象，故左右视差图象都需要得到。
B：控制点集的计算，采取以下方法计算控制点集。
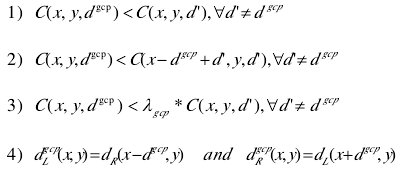
C：初始匹配代价的聚集
首次在极线间分别采取下面两式进行自上而下和自下而上的动态计划计算，然落后行垂直方向的匹配代价积累
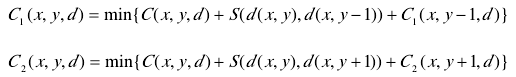
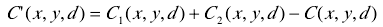
为避免视差图在极线间出现垂直条纹，采取权重方式实现匹配代价的更新。
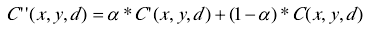
D：基于控制点的双向动态计划
以左图为准时，从左到右搜索最优路径，以右图为准时，从右到左搜索最优路径。当路径到达控制点时，记录下控制点处的视差值，用来束缚控制点后面像素的能量函数计算，进而到达束缚后面像素的视差结果的作用。非控制点处，左右极线上分别进行动态计划的计算，然后利用动态计划回溯的方法寻觅每一个像素的视差。
计算出左右视差图象后，根据弱1致性束缚，当左视差图象中的某点视差大于右视差图象对应点的视差时采取其对应点的视差取代，这样可以有效的处理半遮挡及前景物体区域的误匹配。
对无纹理区域的误匹配利用同区域已匹配点的视差填充。
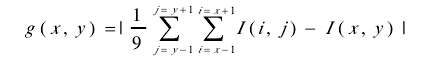
对大视差的图象对误差比较大。
若求取的控制点个数为C，那末控制点的采取可使传统复杂度由O(MND*D)下降为O((MN-C)D*D)，取得的控制点越多，动态计划的计算复杂度越小。
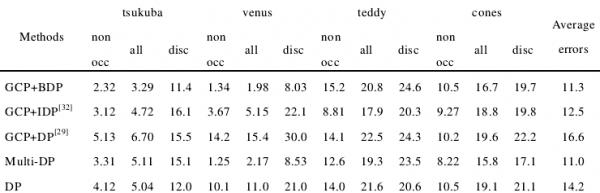
在论文中看到的测试结果
