浅谈小波分析
- 小波的发展历史与驱动
- 傅里叶变换
- 短时傅里叶变换
- 小波变换
- 傅里叶变换
- 小波变换
- 3种变换的对照
- 小波变换
- 离散小波变换
- 连续小波变换
- 小波的多分辨率论述
- 信号空间
- 尺度函数
- 多分辨率分析
- 多分辨率流程
- 其他
- 突变信号与吉布斯效应
- 海森堡不肯定原理
- 降维
- 窗口化
- 参考资料
本文首先介绍了从傅里叶变换到小波变换的发展史,然后侧重强调了小波变换的两种作用——时频分析和多分辨率分析,最后讲了1下吉布斯效应等相干知识。
小波的发展历史与驱动
傅里叶变换
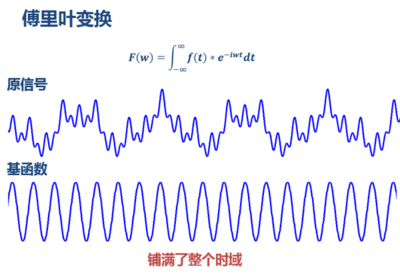
FT(傅里叶变换),通过将信号分解成正余弦函数(把3角函数当作函数空间的基),将时域信号转化为频域信号。缺点是只适用于安稳性信号,在频域图上不能取得对应频率的时间信息。
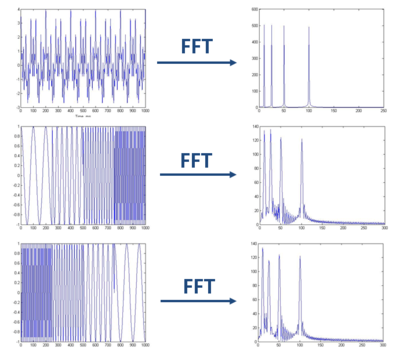
由上图可以看到,对频域成份相同的信号,即便信号在时域上的散布不1样,FFT变换后的频域图却几近完全1样。所以说,FFT只可以取得1段信号整体上包括哪些成份,但是对各成份出现的时间并没有所知。因此时域相差很大的信号FFT以后的频域图可能完全相同。
短时傅里叶变换
STFT(短时傅里叶变换)添加时域信息的方法是设置窗格,认为窗格内的信号是安稳信号,对窗格内的信号分段进行FT分析。优点是可以取得频域信息的同时可以取得时域信息。缺点是窗格大小很难设置。
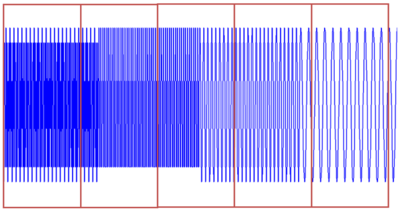
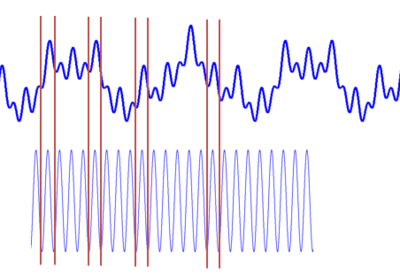
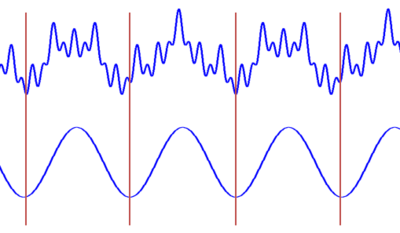
STFT的方法及效果以下图:
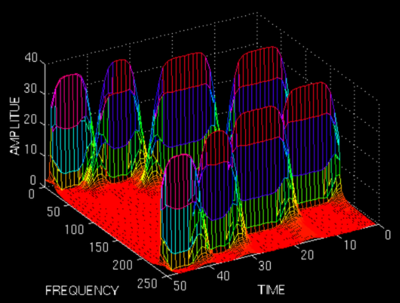
STFT的窗格问题以下:
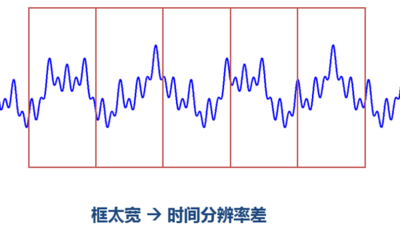
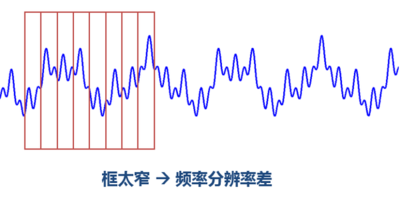

由上面的图可以看到,窄窗口时间分辨率高、频率分辨率低;宽窗口时间分辨率低,频率分辨率高。对时变的非稳态信号,高频合适小窗口,低频合适大窗口。可是STFT的窗口是固定的,因此需要寻求别的方法。
小波变换
WT(小波变换),将傅里叶变换的基给换了—— 将无穷长的3角函数基换成了有限长的会衰减的小波基,这样不但可以获得频率,还可以定位到时间。
傅里叶变换
傅里叶变换,通过相互正交的3角函数信号和原信号在无穷上进行积分,积分越大表明信号越类似,包括该频率的3角信号也就越多。
最后,每个f值对应了1个积分值,取得了频率图。
小波变换
小波变换的原理类似傅里叶变换,只是把3角函数基换成了小波基。
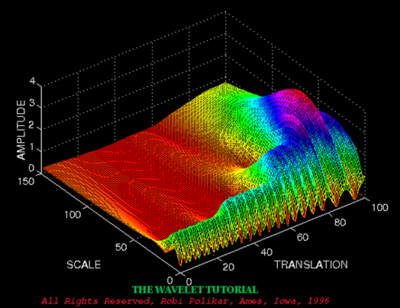
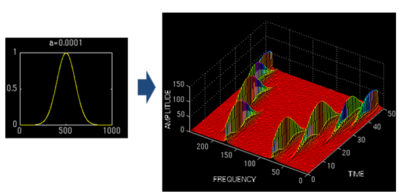
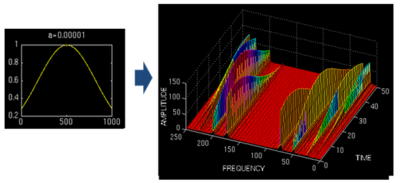
与傅里叶变换不同,小波变换有两个变量:scale和translation。scale控制小波函数的收缩,其导数即为频率,translation控制小标函数的平移,平移量对应时间。
通过信号的伸缩平移,可以得到某种重合情况,这样积分也会得到1个极大值,不同的是,得到频率成份的同时,还可以知道该频率的时间位置。

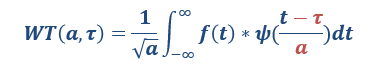
.png)
最后得到的也是3维的图象:

3种变换的对照
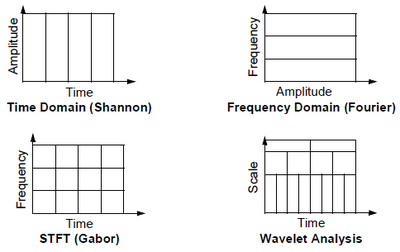
傅里叶变换,选择正弦函数作为基函数,然后考察的到的展开式的性质。
对小波分析,首先提出想要的性质,然后推导出基函数。
小波变换
离散小波变换
连续小波变换
小波的多分辨率论述
小波的1个思想是在时间和频率两个方面提供有效的局部化,另外一个中心思想是多分辨率,即信号的分解是依照不同分辨率的细节1层1层进行的。
信号空间
尺度函数
对2维函数族(构成空间的基底):
对所有
如果
也就是说,
多分辨率分析
低分辨率上的信号,不但可以通过该低分辨率上的信号基底组合,还可以通太高分辨率上信号的基底组合起来。
尺度函数