动态规划 最长公共子序列 过程图解

1.基本概念

      首先需要科普1下，最长公共子序列（longest common sequence）和最长公共子串（longest common substring）不是1回事儿。甚么是子序列呢？即1个给定的序列的子序列，就是将给定序列中零个或多个元素去掉以后得到的结果。甚么是子串呢？给定串中任意个连续的字符组成的子序列称为该串的子串。给1个图再解释1下：

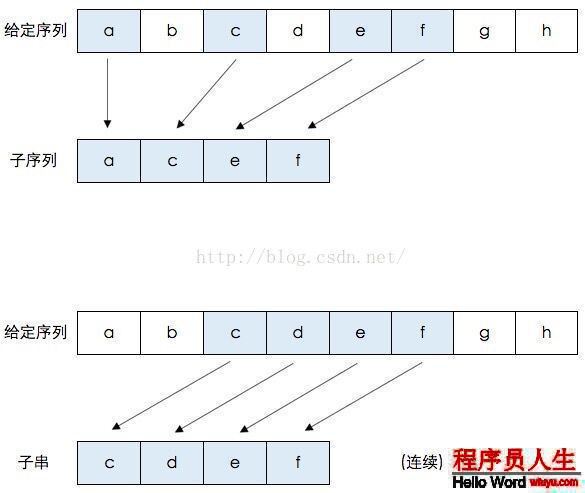
       如上图，给定的字符序列： {a,b,c,d,e,f,g,h}，它的子序列示例： {a,c,e,f} 即元素b,d,g,h被去掉后，保持原本的元素序列所得到的结果就是子序列。同理，{a,h},{c,d,e}等都是它的子序列。
       它的字串示例：{c,d,e,f} 即连续元素c,d,e,f组成的串是给定序列的字串。同理，{a,b,c,d},{g,h}等都是它的字串。

        这个问题说明白后，最长公共子序列（以下都简称LCS）就很好理解了。
给定序列s1={1,3,4,5,6,7,7,8},s2={3,5,7,4,8,6,7,8,2}，s1和s2的相同子序列，且该子序列的长度最长，即是LCS。
s1和s2的其中1个最长公共子序列是 {3,4,6,7,8}

2.动态计划

       求解LCS问题，不能使用暴力搜索方法。1个长度为n的序列具有 2的n次方个子序列，它的时间复杂度是指数阶，太恐怖了。解决LCS问题，需要借助动态计划的思想。
       动态计划算法通经常使用于求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解。每个解都对应于1个值，我们希望找到具有最优值的解。动态计划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，合适于用动态计划求解的问题，经分解得到子问题常常不是相互独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很屡次。如果我们能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就能够避免大量的重复计算，节省时间。我们可以用1个表来记录所有已解的子问题的答案。不管该子问题以后是不是被用到，只要它被计算过，就将其结果填入表中。这就是动态计划法的基本思路。

3.特点分析

       解决LCS问题，需要把原问题分解成若干个子问题，所以需要刻画LCS的特点。

       设A=“a0，a1，…，am”，B=“b0，b1，…，bn”，且Z=“z0，z1，…，zk”为它们的最长公共子序列。不难证明有以下性质：
       如果am=bn，则zk=am=bn，且“z0，z1，…，z(k⑴)”是“a0，a1，…，a(m⑴)”和“b0，b1，…，b(n⑴)”的1个最长公共子序列；
       如果am!=bn，则若zk!=am，蕴涵“z0，z1，…，zk”是“a0，a1，…，a(m⑴)”和“b0，b1，…，bn”的1个最长公共子序列；
       如果am!=bn，则若zk!=bn，蕴涵“z0，z1，…，zk”是“a0，a1，…，am”和“b0，b1，…，b(n⑴)”的1个最长公共子序列。

       有些同学，1看性质就容易晕菜，所以我给出1个图来让这些同学理解1下：

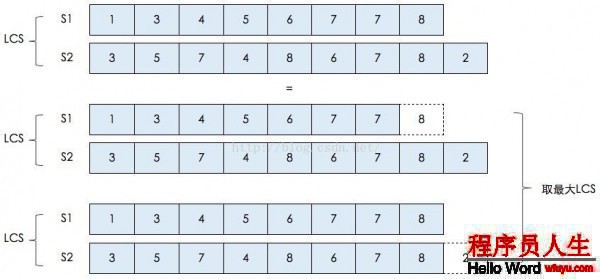
       以我在第1小节举的例子（S1={1,3,4,5,6,7,7,8}和S2={3,5,7,4,8,6,7,8,2}），并结合上图来讲：

       假设S1的最后1个元素 与 S2的最后1个元素相等，那末S1和S2的LCS就等于 {S1减去最后1个元素} 与 {S2减去最后1个元素} 的 LCS  再加上 S1和S2相等的最后1个元素。

       假设S1的最后1个元素 与 S2的最后1个元素不等（本例子就是属于这类情况），那末S1和S2的LCS就等于 ： {S1减去最后1个元素} 与 S2 的LCS， {S2减去最后1个元素} 与 S1 的LCS 中的最大的那个序列。

4.递归公式

        第3节说了LCS的特点，我们可以发现，假定我需要求 a1 ... am 和 b1 .. b(n⑴)的LCS 和 a1 ... a(m⑴) 和 b1 .. bn的LCS，1定会递归地并且重复地把如a1... a(m⑴) 与 b1 ... b(n⑴) 的 LCS 计算几次。所以我们需要1个数据结构来记录中间结果，避免重复计算。

        假定我们用c[i,j]表示Xi 和 Yj 的LCS的长度（直接保存最长公共子序列的中间结果不现实，需要先借助LCS的长度）。其中X = {x1 ... xm}，Y ={y1...yn}，Xi = {x1 ... xi}，Yj={y1... yj}。可得递归公式以下：

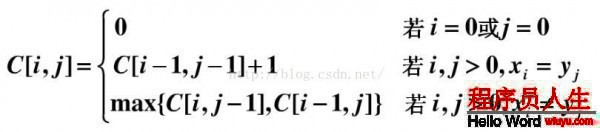
5.计算LCS的长度

       这里我不打算贴出相应的代码，只想把这个进程说明白。还是以s1={1,3,4,5,6,7,7,8},s2={3,5,7,4,8,6,7,8,2}为例。我们借用《算法导论》中的推导图：

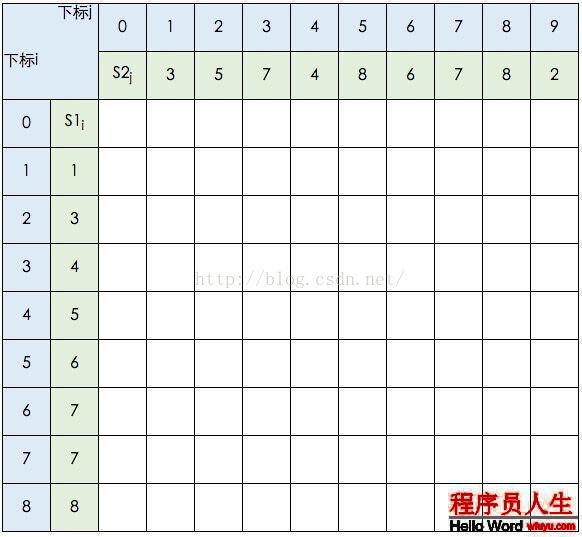
         图中的空白格子需要填上相应的数字（这个数字就是c[i,j]的定义，记录的LCS的长度值）。填的规则根据递归公式，简单来讲：如果横竖（i,j）对应的两个元素相等，该格子的值 = c[i⑴,j⑴] + 1。如果不等，取c[i⑴,j] 和 c[i,j⑴]的最大值。首先初始化该表：

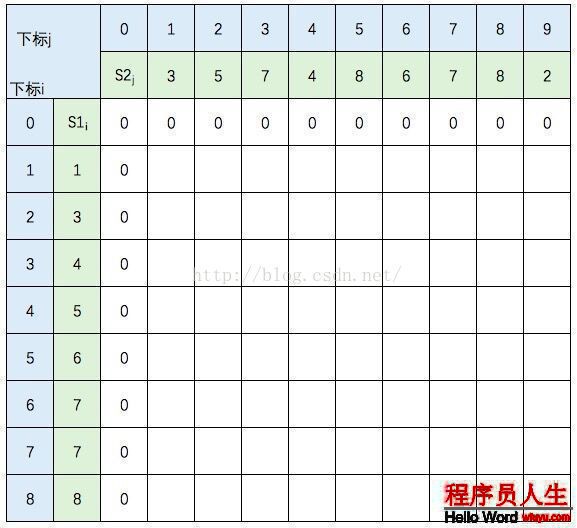
          然后，1行1行地从上往下填：

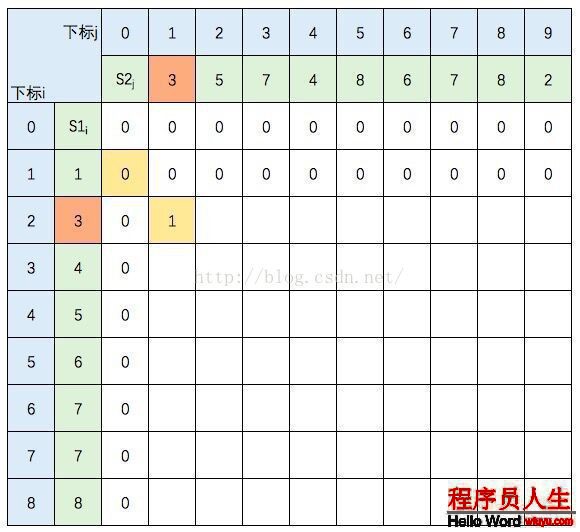
          S1的元素3 与 S2的元素3 相等，所以 c[2,1] = c[1,0] + 1。继续填充：

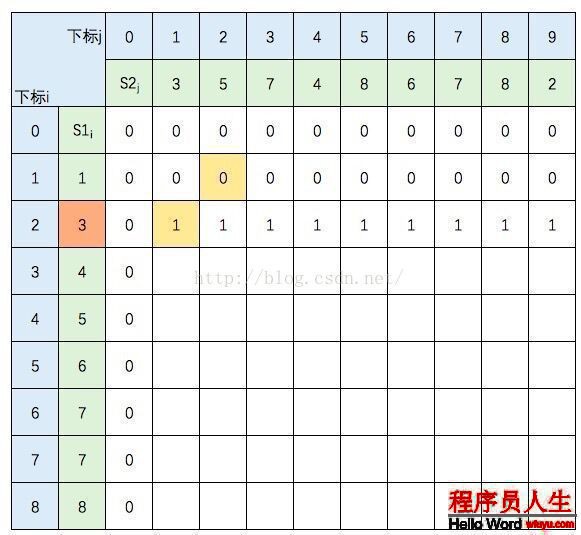
            S1的元素3 与 S2的元素5 不等，c[2,2] =max(c[1,2],c[2,1])，图中c[1,2] 和 c[2,1] 背风景为浅黄色。

            继续填充：

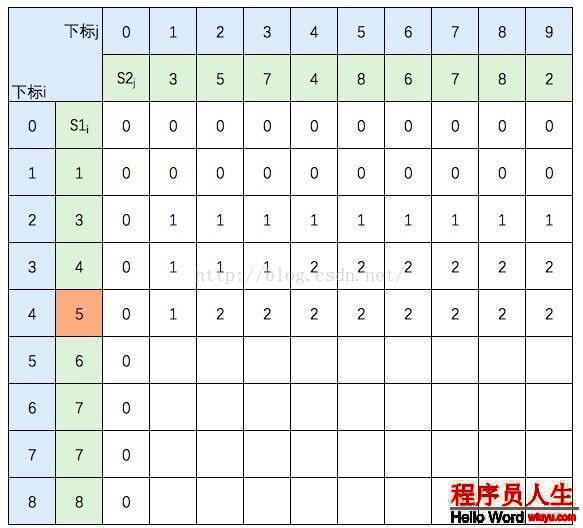
               中间几行填写规则不变，直接跳到最后1行：

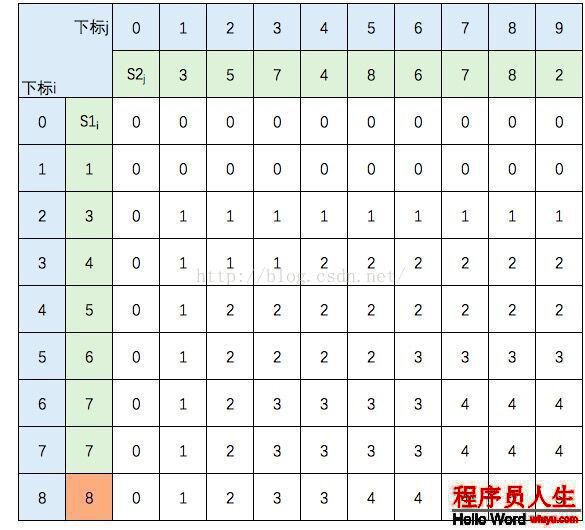
                至此，该表填完。根据性质，c[8,9] = S1 和 S2 的 LCS的长度，即为5。

6.构造LCS

       本文S1和S2的最LCS其实不是只有1个，本文其实不是侧重讲输出两个序列的所有LCS，只是介绍如何通过上表，输出其中1个LCS。

       我们根据递归公式构建了上表，我们将从最后1个元素c[8][9]倒推出S1和S2的LCS。

       c[8][9] = 5，且S1[8] != S2[9]，所以倒推回去，c[8][9]的值来源于c[8][8]的值(由于c[8][8] > c[7][9])。

       c[8][8] = 5,  且S1[8] = S2[8], 所以倒推回去，c[8][8]的值来源于 c[7][7]。

       以此类推，如果遇到S1[i] != S2[j] ，且c[i⑴][j] = c[i][j⑴] 这类存在分支的情况，这里请都选择1个方向（以后遇到这样的情况，也选择相同的方向）。

       第1种结果为：

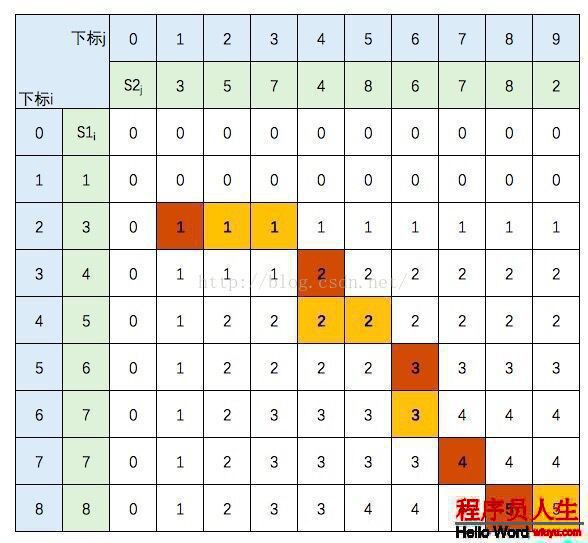
          这就是倒推回去的路径，棕色方格为相等元素，即LCS = {3,4,6,7,8}，这是其中1个结果。

          如果如果遇到S1[i] != S2[j] ，且c[i⑴][j] = c[i][j⑴] 这类存在分支的情况，选择另外一个方向，会得到另外一个结果。

           即LCS ={3,5,7,7,8}。

7.关于时间复杂度

        构建c[i][j]表需要Θ(mn)，输出1个LCS的序列需要Θ(m+n)。

          本文内容参考以下：

        【1】http://baike.baidu.com/link?url=iKrtEZXAQ3LeQLL7Z0HQWpy7EO7BZInUR17C63lAIDFBJ_COm8e3KmKVxQCD6DlOvji2F9W6achz49Z_anZCfa

        【2】《算法导论》第3版 15.4节

        注意：
        如您发现本文档中有明显毛病的地方，
        或您发现本文档中援用了他人的资料而未进行说明时，请联系我进行更正。
        转载或使用本文档时，请作醒目说明。
        必要时请联系作者，否则将追究相应的法律责任。

        note:
        If you find this document with any error ,
        Or if you find any illegal citations , please contact me correct.
        Reprint or use of this document,Please explain for striking. 
        Please contact the author if necessary, or they will pursue the corresponding legal responsibility.