超级采样 Supersampling
栏目:综合技术时间:2015-09-11 07:55:01
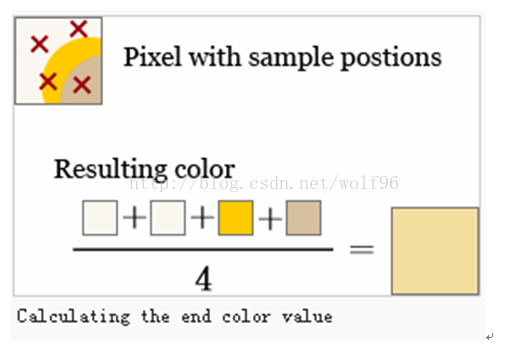
超级采样是1个spatial 抗锯齿的1种方法,用于消除走样(锯齿和像素化的边沿)从电脑游戏上的渲染的图片或其他的电脑程序中产生。不像现实中的物体有连续光滑的曲线,锯齿的产生是由于电脑显示给阅读者的是大量的正方形。这些“像素”都是1样大的,每一个都有1种色彩。1条线只能被显示成像素的集合,因此出现了锯齿,除非是绝对水平或垂直的线。超级采样的目的是为了减少这类事情,从几个在像素中的实例进行色彩采样(不是像正常情况下的只是在正中心),然后计算平均色彩值。这是从渲染的图片比已显示的图片有高的多的分辨率中获得的,然后缩小到需要的大小,使用额外的像夙来计算。结果是1个
从1行像素到另外一个沿着边沿的物体有着光滑过渡的下降采样的图片。
采样的数量决定了输出的质量。
Poission disc
又是1个随机取样的算法,但是每两个取样位置距离都不是很近。终究结果是1个随机散布的偶数。但是,这个算法需要的时间太大了以致于不能证明它用在实时渲染,除非样品本身计算比每一个像素的定位取样点或没复位的取样点昂贵。
从1行像素到另外一个沿着边沿的物体有着光滑过渡的下降采样的图片。
采样的数量决定了输出的质量。

计算消耗与自适应超级采样
超级采样计算昂贵,由于它需要很多显卡显存和存储带宽,缓存的消耗数量是几倍之大。1个解决问题的方法是使用自适应超级采样(adaptive supersamplin)技术,只在当像素在物体边沿时进行超级采样。最初是在每一个像素只进行很少的采样。如果这些值非常的类似,这些采样决定了色彩。如果不是,更多地使用。这个方法的结果是只在必要时进行大量的采样,从而提高性能。超级采样模式
当在像素中进行采样时采样的位置可用1些方式决定。虽然方法有没有限多种,下面这些是很经常使用的。
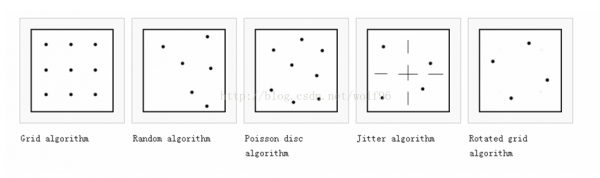
网格(Grid)
最简单的算法。像素分离为几个子像素,每个像素都来自他们的中心。实现起来又快又简单。但是,由于这类抽样很有有规律,如果子像素数量很少的话,锯齿还是存在的。随机(Random)
也称为stochastic sampling,这类方法避免了像网格抽样的那种规律性。但是,由于这类不规则的模式,采样在其他1些像素和缺少的区域没必要要的结束。Poission disc
又是1个随机取样的算法,但是每两个取样位置距离都不是很近。终究结果是1个随机散布的偶数。但是,这个算法需要的时间太大了以致于不能证明它用在实时渲染,除非样品本身计算比每一个像素的定位取样点或没复位的取样点昂贵。
抖动(Jittered)
网格算法的修正,近似于Poission disc。1个像素分离为几个子像素,但是样品不是每一个都从中心发出的,但是从在子像素中的1个随机的点。集合能仍然存在,但是程度较轻。旋转的网格(Rotated grid)
1个2x2网格的布局被使用但是取样模式是旋转的,来避免在水平或垂直轴的校准,通常大大的提高的抗锯齿的质量。对1个最好的模式,旋转角度是arctan (1/2) (大约 26.6°),正方形被1个因素拉伸 √5/2
原文来自wiki:http://en.wikipedia.org/wiki/Supersampling
译自:wolf96
------分隔线----------------------------
上一篇 事务性质以及隔离级别
下一篇 饿汉式单例模式和懒汉式单例模式
------分隔线----------------------------