程序员人生网站导航

[Python] 机器学习库 Scikit-learn之SVM

栏目：综合技术时间：2015-06-04 08:11:56

0. SVM简介

SVM是最经常使用的分类器之1，其可以用来做分类，回归和异常检测。
其模型定义和学习以下：
原始问题:

$min_ {w, b, zeta} frac{1}{2} w^T w + C sum_{i=1}^{n} zeta_i$

$extrm {subject to } y_i (w^T phi (x_i) + b) geq 1 - zeta_i,$

$zeta_i geq 0, i=1, ..., n$

对偶问题：

$min_{alpha} frac{1}{2} alpha^T Q alpha - e^T alpha$

subject to $y^T alpha = 0$

$0 leq alpha_i leq C, i=1, ..., n$

决策函数：

$operatorname{sgn}(sum_{i=1}^n y_i alpha_i K(x_i, x) + ho)$

其中 $e$ 是全为1的向量, $C > 0$ 是上边界, $Q$ 是 $n$ $imes$ $n$ 半正定矩阵, $Q_{ij} equiv K(x_i, x_j) = phi (x_i)^T phi (x_j)$ 是核，训练数据通过 $phi$ 被映照到高纬空间中.

svm的优点：

在高纬空间的有效性。
在特点维度高于样本维度的情况下，仍然有效。
它的决策函数只使用训练数据的1部份，通常把这1部份数据称之为支持向量，所以它是比较节省内存的。
可以提供各种各样的核函数来扩大SVM的功能。

SVM的缺点：

如果特点的维度远大于样本的数目，那末性能将大大的下降。
SVM不直接提供几率估计。

1. SVM用来做分类：

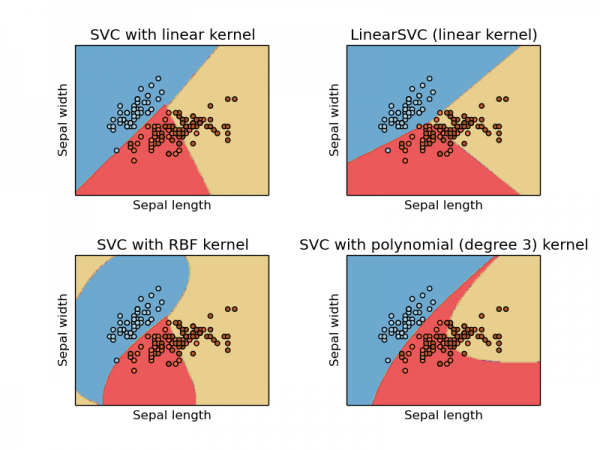
SVC, NuSVC，LinearSVC

这3类都能用来做多类分类，SVC 和 NuSVC 类似，但是在1些参数上有所不同，LinearSVC 则是另外1种svm的实现，它是线性核。
这里写图片描述

输入：

SVC, NuSVC 和LinearSVC的输入训练数据：[n_samples, n_features] ，标签数据：[n_samples]，标签可以是整数或是字符串都可以。

#训练svm：
>>> from sklearn import svm
>>> X = [[0, 0], [1, 1]]
>>> y = [0, 1]
>>> clf = svm.SVC()
>>> clf.fit(X, y) `
#测试svm`
>>> clf.predict([[2., 2.]

成员变量：

由于svm模型只需要用到训练数据中的1部份，也就是支持向量的部份。
support_vectors_：寄存模型的支持向量。
support_ ：寄存模型的支持向量的索引。
n_support: 寄存模型每类的支持向量的数目。

多类分类

原始的svm只能支持2类的分类，而多类分类是通过量次2分类来实现的，具体有两种方式，即1对1和1对多两种方式。
SVC 和 NuSVC是采取1对1的方式，如果 n_class 是总的种别的数目，那末共需要训练n_class * (n_class - 1) / 2 个不同的2分类器。

#获得分类器的数目：
X = [[0], [1], [2], [3]]
Y = [0, 1, 2, 3]
clf = svm.SVC()
clf.fit(X, Y)
dec = clf.decision_function([[1]])
print dec.shape[1]

不同的是， LinearSVC 是采取1对多的方式来进行多分类，具体来讲，有 n_class 个种别就训练n_class 个分类器，明显，在了种别数目比较多的情况下，这样更节省空间和时间。

不平衡数据：

SVC实现了不平衡训练数据集上的处理，通过设置class_weight参数来给每一个种别设置不同的权重，具体的使用还得看文档。

2. SVM用来做回归

SVM分类器可以很自然的被扩大用来做回归，被称之为支持向量回归。
SVR跟SVC1样，模型只斟酌支持向量的数据，那些原理分界边际的点将被忽视。
跟SVC类似，其也有3个类来显示它，对应的是： SVR, NuSVR ， LinearSVR，

>>> from sklearn import svm
>>> X = [[0, 0], [2, 2]]
>>> y = [0.5, 2.5]
>>> clf = svm.SVR()
>>> clf.fit(X, y) 
SVR(C=1.0, cache_size=200, coef0=0.0, degree=3, epsilon=0.1, gamma=0.0,
    kernel='rbf', max_iter=-1, shrinking=True, tol=0.001, verbose=False)
>>> clf.predict([[1, 1]])
array([ 1.5])

3. 密度估计，异常检测

种别：OneClassSVM 来实现异常检测，这是1种无监督的方法，它的训练数据只需要 $X$ ,而无需 $Y$ 。

4. 复杂度分析

SVM是1个2次计划问题（QP问题），其实重训练数据集合中分离出支持向量的数据点，在基于libsvm的实现中，其复杂度介于： $O(n_{features} imes n_{samples}^2)$ 和 $O(n_{features} imes n_{samples}^3)$ 之间。

5. 核函数

? 线性核: $langle x, x' angle$ .

? 多项式核: (γ?x,x′?+r)

------分隔线----------------------------

上一篇 文件流程的操作

下一篇 java操作svn【svnkit】实操

------分隔线----------------------------