汉诺塔递归算法理解及实现
汉诺塔:(Hanoi)是1种玩具,如图:

从左到右 A B C 柱 大盘子在下, 小盘子在上, 借助B柱将所有盘子从A柱移动到C柱, 期间只有1个原则: 大盘子只能在小盘子的下面.
问题理解与描写:
1.问题的理解与描写
问题的情势化表示为:
输入:圆盘数n,3根细杆―― 源杆A、过渡杆B和目标杆C。
输出:圆盘从源杆移动到目标杆进程的最少步骤序列。
2.算法的伪代码:
HANOI(n, A, B, C)
1 if n=1
2 then print A,"?", C
3 return
4 HANOI(n-1,A, C, B)
5 print A,"?", C
6 HANOI(n-1,B, A, C)3.算法的运行时间:
对盘数n,HANOI进程的运行时间
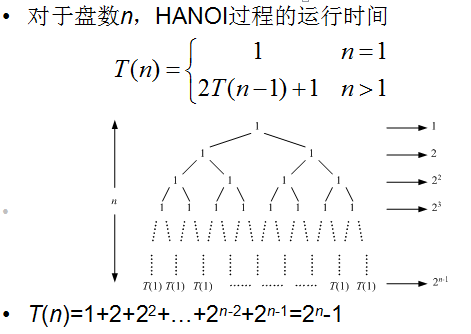
4 算法理解:
理解1:(参考:http://blog.csdn.net/yafei450225664/article/details/8647908)
案例 1 - 假定只有1个盘子的时候, 盘子数量 N=1
只有1个步骤 将第1个盘子从A移动到C, 为了对照方便我这样来描写这个步骤:
步骤 盘子编号 从柱子移动 移动到柱子
1 1 A C
案例 2 - 如果有两个盘子, 盘子数量 N = 2
步骤 盘子编号 从柱子移动 移动到柱子
1 1 A B
2 2 A C
3 1 B C
案例 3 - 如果有3个盘子, 盘子数量 N = 3
步骤 盘子编号 从柱子移动 移动到柱子
1 1 A C
2 2 A B
3 1 C B
4 3 A C
5 1 B A
6 2 B C
7 1 A C
如何找出盘子移动的规律 ?
我们要做的最重要的1件事情就是永久要把最底下的1个盘子从 A 移动到 C
看看上面从1个盘子的移动到3个盘子的移动, 在移动记录中,当盘子的编号和盘子数量相同的时候他们的步骤都是从A移动到C (看加粗的部份),其它的步骤对等.
再视察第3个案例中的第 1⑶ 步 和 第 5⑺步
第 1⑶ 步 目的是从 A 移动到 B 如果我们把 B 当作终点, 那末这里的第 1⑶ 步理解起来和 第2个案例的3个步骤完全相同, 都是通过1个柱子来移动,和第2个案例比起来在后面加括号来表示
1 1 A C ( A -> B)
2 2 A B ( A -> C)
3 1 C B ( B -> C)
总结:将盘子B变成C便可.
第 5⑺ 步 目的是从 B 移动到 C 如果我们把 C 当作终点, 那末这里的 5⑺ 步理解起来和上面也是1样的, 和第2个案例的3个步骤也完全相同.和第2个案例比起来就是:
5 1 B A ( A -> B)
6 2 B C ( A- > C)
7 1 A C ( B -> C)
总结: 将盘子B变成A便可
根据这个演示可以明确几点规律:
1. 当盘子只有1个的时候,只有1个动作 从 A 移动到 C 即结束.
2. 当有N个盘子的时候, 中间的动作都是从 A 移动到 C, 那末表示最下面的第N个盘子移动终了
3. 中间动作之上都可以认为是: 从 A 移动到 B
4. 中间动作之下都可以认为是: 从 B 移动到 C
2,3,4 可以表示为
1 1 A B
2 2 A C
3 1 B C
理解2:(参考:http://blog.csdn.net/leo115/article/details/7991734)
美国的1位学者发现1种出人意料的简单的算法,只要轮番两步操作既可以实现:首先,把3张桌子按顺序首尾相接的排列,构成1个环,然后对A上的盘子开始移动,顺时针摆放成 A B C的顺序:
若n为奇数,圆盘的移动顺序是 A->C->B->A->C->B->A……… 即 间隔两个步长移动 。此处的n代表盘子位的层数,比如说 3 层汉诺塔就是从下往上数第1、3 个盘子移动的顺序。
若n为偶数,圆盘移动的顺序为A->B->C->A->B->C->A……….即 间隔1个步长移动。对n的解释同上 第2个盘子移动 A->B->C。
5.代码实现(c):
/*************hanoi.c********************/
#include<stdlib.h>
#include <stdio.h>
#include "hanoi.h"
/*************找x杆顶部盘的编号**********
输入参数:current[i]记录第i号盘所在的杆号
x;杆的编号
输出参数:x杆顶部盘的编号
****************************************/
int pickTopDisk(char* current,char x)
{
int i = 0;
while (current[i] != x)
i++;
return i;
}
/*************汉诺塔**********
输入参数:current[i]记录第i号盘所在的杆号
n:盘的数量
A,B,C:杆的编号
****************************************/
void hanoi(char* current, int n, char A, char B, char C)
{
static int cout = 0; //static类型变量会在函数屡次调用时保存改变的值,并且初始化操作仅做1次
int i = 0;
if (n==1)
{
i = pickTopDisk(current, A);
current[i] = C;
cout++;
printf("move %d disk %d: %c->%c
", cout, i + 1, A, C);
return;
}
hanoi(current, n - 1, A, C, B);
current[n- 1] = C;
cout++;
printf("move %d disk %d: %c->%c
", cout, n, A, C);
hanoi(current, n - 1, B, A, C);
}/****************hanio.h************/
#ifndef _HANOI_H
#define _HANOI_H
#ifdef __cplusplus
extern "C" {
#endif // __cplusplus
int pickTopDisk(char* current, char x);
void hanoi(char* current, int n, char A, char B, char C);
#ifdef __cplusplus
}
#endif
#endif/**************main.c************************/
#include <stdlib.h>
#include "hanoi.h"
int main(int argc, char** argv)
{
char current[] = { 'A', 'A', 'A', 'A' };
char A = 'A', B = 'B', C = 'C';
hanoi(current, 4, A, B, C);
system("pause");
return EXIT_SUCCESS;
}6运行结果:
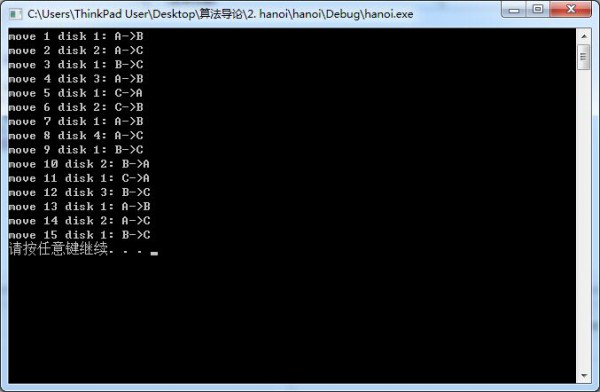
参考:《算法设计、分析与实现:C、C++和Java》 徐子珊