(高效率排序算法一)并归排序
栏目:综合技术时间:2015-05-21 07:54:26
归并排序
归并排序是建立在归并操作上的1种有效的排序算法,该算法是采取分治法(Divide
and Conquer)的1个非常典型的利用。将已有序的子序列合并,得到完全有序的序列;即先使每一个子序列有序,再使子序列段间有序。若将两个有序表合并成1个有序表,称为2路归并。
归 并进程为:比较a[i]和a[j]的大小,若a[i]≤a[j],则将第1个有序表中的元素a[i]复制到r[k]中,并令i和k分别加上1;否则将第2 个有序表中的元素a[j]复制到r[k]中,并令j和k分别加上1,如此循环下去,直到其中1个有序表取完,然后再将另外一个有序表中剩余的元素复制到r中 从下标k到下标t的单元。归并排序的算法我们通经常使用递归实现,先把待排序区间[s,t]以中点2分,接着把左侧子区间排序,再把右侧子区间排序,最后把左
区间和右区间用1次归并操作合并成有序的区间[s,t]。
中文名:归并排序
外文名:Merge sort
稳定性:稳定
时间复杂度:O(n log n)
空间复杂度:O(n)
发明者:约翰・冯・诺伊曼
(速度仅次于快速排序,为稳定排序算法,1般用于对整体无序,但是各子项相对有序的数列,利用见2011年普及复赛第3题“瑞士轮”的标程)
快速排序流程效果以下,下次再写它
快速排序流程效果以下,下次再写它
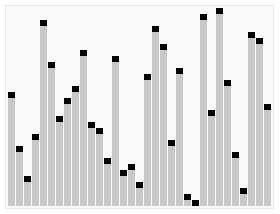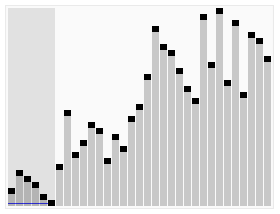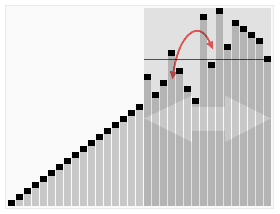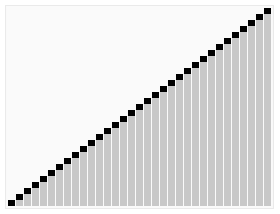
归并操作
归并操作(merge),也叫归并算法,指的是将两个顺序序列合并成1个顺序序列的方法。
如 设有数列{6,202,100,301,38,8,1}
初始状态:6,202,100,301,38,8,1
第1次归并后:{6,202},{100,301},{8,38},{1},比较次数:3;
第2次归并后:{6,100,202,301},{1,8,38},比较次数:4;
第3次归并后:{1,6,8,38,100,202,301},比较次数:4;
总的比较次数为:3+4+4=11,;
逆序数为14;
下面是我网上找的图
下面是我网上找的图
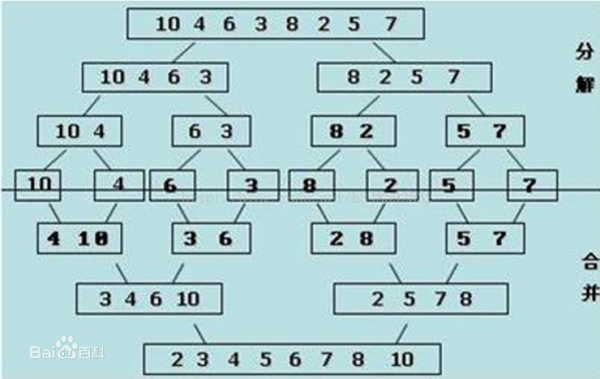
固然我下面写的程序,数组还是同个数组,分解的时候是直接按最小分解开始,就是直接按最细粒度分解
快速排序算法的确比并归算法速度快点
package data;
import java.util.Arrays;
import java.util.Random;
/**
* 并归排序
* @author JYC506
*
*/
public class MergeSort {
/**
* 对部份排好序的数组进行归并
* @param arr 要操作的数组
* @param start1 排好序的数组部份1出发点
* @param end1 排好序的数组部份1终点
* @param start2 排好序的数组部份2出发点
* @param end2 排好序的数组部份2终点
* @return
*/
private static int[] merger(int[] arr, int start1, int end1, int start2, int end2) {
int[] newArr = new int[(end1 - start1) + (end2 - start2) + 2];
int index1 = start1;
int index2 = start2;
int index = 0;
/*比较两个数组排好序的部份,从这两部份开始出发点做比较,比较小的插入新数组
例如比较a[i]和a[j]的大小,若a[i]≤a[j],则将第1个有序表中的元素a[i]复制到r[k]中,并令i和k分别加上1;否则将第2 个有序表中的元素a[j]复制到r[k]中,并令j和k分别加上1,如此循环下去,直到其中1个有序表取完*/
while (index1 <= end1 && index2 <= end2) {
if (arr[index1] < arr[index2]) {
newArr[index] = arr[index1];
index++;
index1++;
} else {
newArr[index] = arr[index2];
index++;
index2++;
}
}
/*然后再将另外一个有序表中剩余的元素复制到r中从下标k到下标t的单元*/
while (index1 <= end1) {
newArr[index] = arr[index1];
index++;
index1++;
}
while (index2 <= end2) {
newArr[index] = arr[index2];
index++;
index2++;
}
return newArr;
}
/**
* 对部份且相邻了排好序的数组进行归并
* @param arr 要操作的数组
* @param start1 排好序的数组部份1出发点
* @param start2 排好序的数组部份2出发点
* @param end2 排好序的数组部份2终点
*/
private static void merger(int[] arr, int start1, int start2, int end2) {
int end1 = start2 - 1;
int[] newArr = merger(arr, start1, end1, start2, end2);
System.arraycopy(newArr, 0, arr, start1, newArr.length);
}
/**
* 并归排序
* @param arr 要操作的数组
* @param start 起始坐标
* @param size 分组后每组的元素数
*/
private static void mergerSort(int[] arr, int start, int size) {
/*由于是成对照较,所以要乘以2*/
int length=arr.length;
int dSize=size*2;
int num=length/dSize;
int residue=length%dSize;
// 归并到只剩1个有序集合的时候结束算法,也是就是余数为0的时候
if(num==0){
return;
}
// 进行1趟归并(注意,第1次并归只有1个元素,就是两两比较时已算排序了)
for(int i=0;i<num;i++){
int sta=start+(size*2)*i;
merger(arr,sta,sta+size,sta+size*2⑴);
}
//将剩下的数和最后1个有序集合归并(这个要注意理解)
if(residue!=0){
merger(arr,length-residue-size*2,length-residue,length⑴);
}
// 递归履行下1趟归并排序,并归元素师成倍增加
mergerSort(arr, 0, 2 * size);
}
/**
*
* @param arr 要操作的数组
*/
public static void mergerSort(int[] arr){
/*默许 起始坐标为0,并且分组元素为1个开始,由于1个是不用排序的*/
mergerSort(arr, 0,1);
}
public static void main(String[] args) {
/*测试并归排序*/
int[] ar1=new int[]{10,4,6,3,8,2,5};
MergeSort.mergerSort(ar1);
System.out.println(Arrays.toString(ar1));
/*测试100万随机数并归排序和java自带快速排序*/
int size=1000000;
int[] arr1=new int[size];
int[] arr2=new int[size];
Random ran=new Random();
for(int i=0;i<size;i++){
int data=ran.nextInt(size);
arr1[i]=data;
arr2[i]=data;
}
long start=System.currentTimeMillis();
MergeSort.mergerSort(arr1);
long end1=System.currentTimeMillis();
Arrays.sort(arr2);
long end2=System.currentTimeMillis();
System.out.println((end1-start));
System.out.println((end2-end1));
}
}
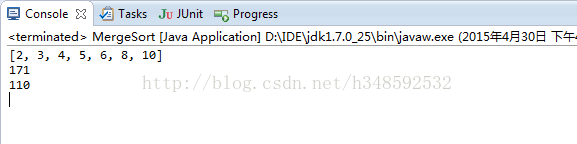
运行结果以下
快速排序算法的确比并归算法速度快点
------分隔线----------------------------
------分隔线----------------------------