Leetcode: Unique Paths
栏目:综合技术时间:2015-04-13 08:22:42
题目:
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
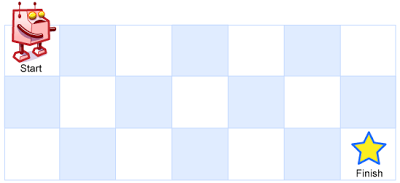
Above is a 3 x 7 grid. How many possible unique paths are there?
Note: m and n will be at most 100.
思路分析:
又是动态计划问题。
开1个f[m][n]的数组,数组元素初始化为1,递推公式f[i][j] = f[i⑴][j] + f[i][j⑴],空间时间复杂度O(m*n)。
(可以将f[m][n]理解成为从f[0][0]到达f[m][n]的路径个数。那很自然的就会f[i][j] = f[i⑴][j] + f[i][j⑴]。有感觉递推公式还不是能很好想出来的,继续加强训练吧!)
C++参考代码:
class Solution
{
public:
int uniquePaths(int m, int n)
{
//将vector中的元素初始化为1
vector<vector<int>> v(m, vector<int>(n, 1));
for (int i = 1; i < m; ++i)
{
for (int j = 1; j < n; ++j)
{
v[i][j] = v[i - 1][j] + v[i][j - 1];
}
}
return v[m - 1][n - 1];
}
};
代码还可以进1步优化。
由C(n,k) = C(n⑴,k) + C(n⑴,k⑴);
对应于杨辉3角:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
………………
所以利用杨辉3角,开1个f[n]的数组,数组元素初始化为1,递推公式f[i]+=f[i⑴],空间时间复杂度O(n)。
class Solution
{
public:
int uniquePaths(int m, int n)
{
vector<int> v(n, 1);
for (int i = 1; i < m; ++i)
{
for (int j = 1; j < n; ++j)
{
v[j] += v[j - 1];
}
}
return v[n - 1];
}
};
------分隔线----------------------------
------分隔线----------------------------