1:剪枝策略的寻觅的方法
1)微观方法:从问题本身动身,发现剪枝条件
2)宏观方法:从整体动身,发现剪枝条件。
3)注意提高效力,这是关键,最重要的。
总之,剪枝策略,属于算法优化范畴;通常利用在DFS 和 BFS 搜索算法中;剪枝策略就是寻觅过滤条件,提早减少没必要要的搜索路径。
2:剪枝算法(算法优化)
1、简介
在搜索算法中优化中,剪枝,就是通过某种判断,避免1些没必要要的遍历进程,形象的说,就是剪去了搜索树中的某些“枝条”,故称剪枝。利用剪枝优化的核心问题是设计剪枝判断方法,即肯定哪些枝条应当舍弃,哪些枝条应当保存的方法。
2、剪枝优化3原则: 正确、准确、高效.原则
搜索算法,绝大部份需要用到剪枝.但是,不是所有的枝条都可以剪掉,这就需要通过设计出公道的判断方法,以决定某1分支的取舍. 在设计判断方法的时候,需要遵守1定的原则.
剪枝的原则
1) 正确性
正如上文所述,枝条不是爱剪就可以剪的. 如果随意剪枝,把带有最优解的那1分支也剪掉了的话,剪枝也就失去了意义. 所以,剪枝的条件是1定要保证不丢失正确的结果.
2)准确性
在保证了正确性的基础上,我们应当根据具体问题具体分析,采取适合的判断手段,使不包括最优解的枝条尽量多的被剪去,以到达程序“最优化”的目的. 可以说,剪枝的准确性,是衡量1个优化算法好坏的标准.
3)高效性
设计优化程序的根本目的,是要减少搜索的次数,使程序运行的时间减少. 但为了使搜索次数尽量的减少,我们又必须花工夫设计出1个准确性较高的优化算法,而当算法的准确性升高,其判断的次数一定增多,从而又致使耗时的增多,这便引出了矛盾. 因此,如何在优化与效力之间寻觅1个平衡点,使得程序的时间复杂度尽量下降,一样是非常重要的. 倘若1个剪枝的判断效果非常好,但是它却需要耗费大量的时间来判断、比较,结果全部程序运行起来也跟没有优化过的没甚么区分,这样就太得不偿失了.
3、分类
剪枝算法依照其判断思路可大致分成两类:可行性剪枝及最优性剪枝.
3.1 可行性剪枝 ―― 该方法判断继续搜索能否得出答案,如果不能直接回溯。
3.2 最优性剪枝
最优性剪枝,又称为上下界剪枝,是1种重要的搜索剪枝策略。它记录当前得到的最优值,如果当前结点已没法产生比当前最优解更优的解时,可以提早回溯。
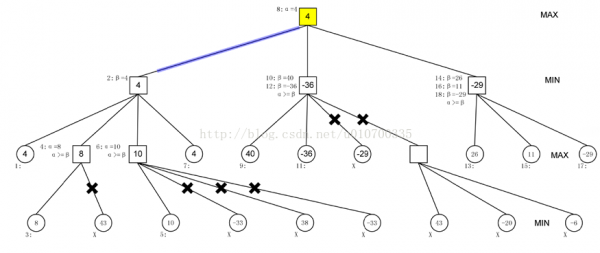
3:示例分析
题目来源于poj 3900 The Robbery (类似于背包问题,但是不能够用背包求解)
1 分析:W,C值很大,数组开不下(所以,不能用背包处理),但是发现N值很小,(1+15)*15/2=120,所以可以斟酌dfs+剪枝。
首先利用贪心的思想我们对箱子进行排序,关键字为性价比(参考了poj里的discuss)。也就是单位重量的价值最高的排第1,搜索的时候枚举顺序注意1定要从满到空,这样才能最快的找到1个可行解然后利用它进行接下来的剪枝。
剪枝1. 以后所有的钻石价值+目前已得到的价值<=ans 则剪枝。
剪枝2. 剩下的重量全部装目前最高性价比的钻石+目前已得到的价值<=ans 则剪枝(非常重要的剪枝)。
2 程序代码
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
#define MY_MAX(a,b) (a)>(b)?(a):(b)
const int maxN = 20;
struct NOTE
{
long long weight;
long long value;
int num;
}box[maxN];
int n;// 个数小于20
long long m,ans;// m 总重量,ans最优解
long long sum[maxN]; //保存1个后缀和
bool cmp(const struct NOTE &a, const struct NOTE &b)
{//按性价比排序,从大到小排列(注意若有取地址符号,则需有const)
return a.value*1.0/a.weight > b.value*1.0/b.weight;
}
inline bool cut (int pos,long long now_value,long long last_weight)
{
if(pos == n+1) return true;//边界返回条件
if(now_value+sum[pos] < ans) return true;////如果后面所有的钻石加起来都<=ans,剪掉
double best = (box[pos].value*1.0/box[pos].weight);//当前最大的性价比
if(now_value+(long long)ceil(best*last_weight) < ans) return true;//以这个性价比取剩下的所有重量,如果<=ans,剪掉
return false;
}
void dfs(int pos,long long now_value,long long last_weight) //pos 当前数组的下标位置,now_value 目前的重量和,last_weight当前背包剩余容量
{
ans = MY_MAX(ans,now_value);
if(cut(pos,now_value,last_weight)) return;//剪枝函数
for(int i=box[pos].num;i>=0;--i)//(暴力搜索)枚举顺序从满到空枚举,这样才能最快找到ans,然后利用ans剪枝
{
if(last_weight<box[pos].weight*i) continue;
dfs(pos+1,now_value+box[pos].value*i,last_weight-box[pos].weight*i);
}
}
int main()
{
int cas;
long long sumv,sumw;// 价值和重量的和;仅仅用到了1次(特殊情况才用到,能够1次全带走)
scanf("%d",&cas);
while(cas--)
{
ans=0;
sumv=sumw=0;
scanf("%d%lld",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%lld",&box[i].weight);
sumw+=box[i].weight*i;
}
for(int i=1;i<=n;i++)
{
scanf("%lld",&box[i].value);
box[i].num=i;
sumv+=box[i].value*i;
}
// 以上是数据的输入,下面才是刚刚开始的
// 如果sumv开始就比m总重量还小,直接输出
if(sumw<=m)
{
printf("%lld
",sumv);
continue;
}
sort(box+1,box+1+n,cmp);// 从1开始计数的
sum[n+1]=0; // 倒着开始的
for(int i=n;i>=1;i--)
{
//计算后缀和
sum[i]=sum[i+1]+box[i].value*box[i].num;
}
dfs(1,0,m);
printf("%lld
",ans);
}
return 0;
}
