[置顶] 动态规划算法分析与探究

动态计划算法分析与探究

摘 要：动态计划是运筹学的1个分支。它是解决多阶段决策进程最优化问题的1种方法。动态计划就是为了使产生决策序列在符合某种条件下到达最优。动态计划思想在各类信息学中频繁的使用，其作用愈来愈遭到人们的重视。本文就动态计划算法进行分析与探究，从而解决实际生活中的诸多问题。

引言

  算法是解决1系列问题的清晰指令，能够在有限的时间内取得所要求的输出。1个好的算法对解决1个或1类实际问题将给予很大帮助。评价1个算法优劣，主要体现在两个方面（排除毛病算法的情况）。1、时间优劣性；2、空间优劣性。时间的优劣即在处理相同问题时，不同算法解决此问题所需的时间。时间的优劣换种方式表达就是算法的效力。另外一方面，是空间优劣即在处理相同问题时，不同算法解决此问题所需占用的资源（计算机资源），主要体现在所占用内存资源上。总的来讲，算法优劣由时间复杂度和空间复杂度来衡量。

   对1种算法，判断是不是是最优算法其实不能单单通过解决1个或1类问题来讲明。由于，对1类的问题也许该算法的复杂度要低于其它算法，而解决另外一类问题的复杂度可能要高于其它算法。因此，没有最好的算法，只有针对某1实际问题有最优的算法，该算法的时间复杂度和空间复杂度要低于其它算法。

1、动态计划简介

   1.1 动态计划基本思想

   动态计划的实质是分治思想和解决冗余，因此，动态计划是1种将问题实例分解为更小的、相似的自问题，并存储子问题的解而避免计算重复的自问题，已解决最优化问题的算法策略。

   动态计划法所针对的问题有1个显著的特点，即它所对应的子问题树中的子问题显现大量的重复。动态计划法的关键就在于，对重复出现的子问题，只在第1次遇到时加以求解，并把答案保存起来，让以后再遇到时直接援用，没必要重新求解。

   1.2动态计划分类

   动态计划按其模型的不同可以分为：背包模型、最长非降子序列模型、最大字段和模型、LCS模型、线段覆盖问题模型、股票模型、连续段划分模型、游戏模型等。其中最为常见的就是背包问题，对背包问题可以再细分为：0⑴背包问题、无穷背包问题、有限背包问题、有价值背包、小数背包等问题。

2、动态计划主要术语

  2.1 阶段

   用动态计划求解1个问题时，需要将问题的全进程恰当地划分成若干个相互联系的阶段，以便按1定的次序去求解。阶段的划分1般是根据时间和空间的自然特点来定的，1般要便于把问题转化成多阶段决策的进程。

   2.2 状态

   状态表示的是事物某1阶段的性质，状态通过1个变量来描写，这个变量称为状态变量。各个状态之间是可以相互转换的。

   2.3 决策

   对问题的处理中做出某种选择性的行动就是决策。1个实际问题可能要有屡次决策，在每个阶段中都需要有1次决策。1次决策就会从1个阶段进入另外一个阶段，状态也就产生了转移。

    2.4策略和最优策略

   所有阶段依照约定的决策方法，顺次排列构成问题的求解全进程。这些决策的整体称为策略。在实际问题中，从决策允许集合中找出最优效果的策略称为最优策略。

   2.5 状态转移方程

前1阶段的终点就是后1阶段的出发点，这类关系描写了由K阶段到K+1阶段状态的演化规律，是关于两个相邻阶段状态的方程，称为状态转移方程，是动态计划的核心。

3、应用动态计划条件

   任何思想方法都有1定的局限性，超越了特定条件，它就失去了作用。同理，动态计划也需满足其使用条件。对解决动态计划问题必须满足最优化原理和无后效性。

  最优化原理：不管过去状态和决策如何，对前面的决策所构成的状态而言，余下的决策必须构成最优策略。简而言之，1个最优化策略的自策略总是最优的。

K

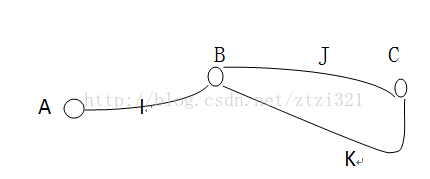
        (图 1)

       如图1所示，线路I和J是A到C的最优路径，则根据最优化原理，线路J必须从B到C的最优线路。

   最优化原理是动态计划的基础，任何问题，如果失去了最优化原理的支持，就不可能用动态计划方法计算。

       无后效性：“过去的步骤只能通过当前状态影响未来的发展，当前的状态是历史的总结”。这条特点说明动态计划只适用于解决当前决策与过去状态无关的问题。状态，出现在策略任何1个位置，它的地位相同，都可实行一样策略，这就是无后效性。

4、动态计划计算步骤

  4.1 划分阶段

   依照问题的时间或空间特点，将问题分为若干个阶段。条件是这个若干个阶段1定要有序，即无后向性。

   4.2 选择状态

   将问题发展到各个阶段时所出现的各种客观情况用不同的状态表示。

   4.3 肯定决策并写出状态转移方程

   状态转移就是根据上1阶段的状态和决策来导出本阶段的状态。

对动态计划问题来讲，阶段的划分是关键，必须根据题意分析，寻求公道的划分阶段的方法。根据计算最优值时得到的信息，构造问题的最优解。

接下来我用1个实例来讲明解决动态计划问题的步骤。

[问题描写]：

设有1个正整数序列b₁，b₂，b₃，…，b_n，若下标为i₁<i₂<i₃<…<i_k且有b_i1≤b_i2≤… ≤b_ik则称存在1个长度为k的不降落序列。可能有多个不降落序列，输出最长序列的长度。

[样例输入]：

13　7　9　16　38　24　37　18

[样例输出]：

5               (7 9  16  24  37)

[问题分析]：

1、    分阶段：以数的个数为阶段。

2、    肯定状态及状态变量：n个数的最长不降落序列长度。

3、    决策：跟前面的哪一个数拼接成最长不降序列。

4、    策略和最优策略：终究解在那。

5、    状态转移方程：

[求解进程]：

1、以个数为阶段，从第2项开始计算，由于前面唯一1项，所以做1次比较，因7<13，不符合问题要求，不作任何改变，长度仍为1。

2、第3项的前面有2项，因此需要做两次比较，得到目前最长的不降落序列为2，情况以下表：

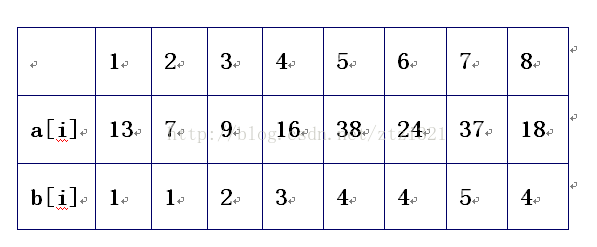
(图 2)

3、处理进程：在1，2，……，i⑴项中，找出比a[i]小于等于的最长长度L；若L>0，则b[i]=L+1。

5、动态计划小结

动态计划所处理的问题是1个“多阶段决策问题”，目的是得到1个最优解（方案）。动态计划的实质是分治思想和解决冗余，因此，动态计划是1种将问题分解为更小的、相似的子问题，并存储子问题的解而避免计算重复的子问题，以解决最优化问题的算法策略。这类问题会有多种可能的解，每一个解都有1个值，而动态计划找出其中最优（最大或最小）解。若存在多个最优解的话，它只取其中的1个。

(图 3)

动态计划与贪心算法类似，是通过量阶段决策进程来解决问题的，同时动态计划又与递归法类似，当问题不能分解为独立的阶段，却又符合最优原理（最优子结构性质）时，就比较合适用动态计划。

但动态计划与1般的递推不同点也比较明显，主要表现以下方面：

1、递推的边界条件1般很明显，而动态计划的边界条件比较隐蔽，容易被忽视；

2、递推的数学性1般较强，而动态计划的数学性相对较弱；

3、递推1般不划分阶段，而动态计划1般有较为明显的阶段；

4、动态计划常常是用来求1个最优值，而1般的递推常常是用来计数或是求1个值。

因此，总的来讲，动态计划更加合适解决绝大多数最优化问题。但是，动态计划来解决问题其实不1定是最优（复杂度较低），因此，具体问题需要具体分析，从而肯定最优算法。