Coursera Machine Learning 学习笔记（八）

IV. Linear Regression with Multiple Variables (Week 2)

- Multiple features

       之前我们介绍了单变量/单特点的回归模型，现在我们对房价预测模型增加更多的变量也就是更多的特点，比如房间数、楼层、房龄等，从而构成1个含有多个变量/特点的模型。

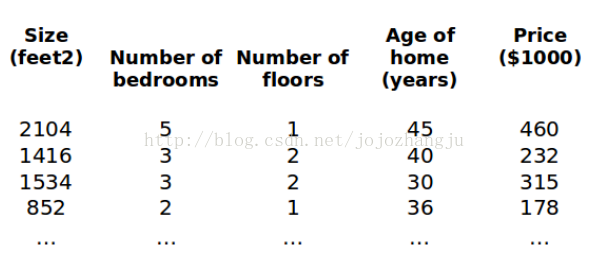
       在增加了更多变量/特点以后，我们将引入1系列新的符号和解释：

       n 代表变量/特点的个数 

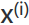       代表第i个训练实例，也就是特点矩阵中的第i行，即1个向量

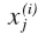       代表第i个训练实例的第j个特点，也就是特点矩阵中第i行的第j个特点

       因此，多变量/特点的假定h可以表示为：

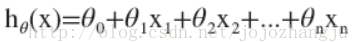
       这个公式中有n+1个参数和n个变量，为了简化公式，我们令，则公式则表示为：

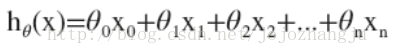
       此时h中的参数是1个n+1维的向量，训练实例也都是n+1维的向量。

       因此公式可以简化为：

       其中上标T代表了矩阵的转置。

- Gradient descent for multiple variables

       与单变量/特点线性回归相似，在多变量/特点线性回归中，我们也将定义1个代价函数，即：

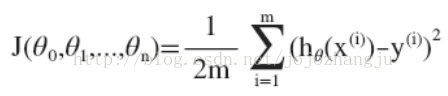
       我们的目标和单变量/特点线性回归中的问题相同，就是要找出使得代价函数最小的参数组合。

       因此，多变量/线性回归梯度降落算法为：

       即：

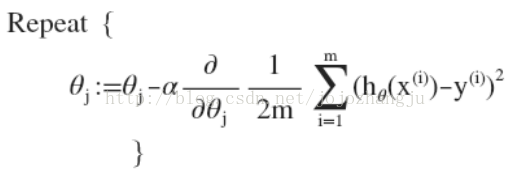
       求导数后可以得到：

       以后，我们通过随机更新1系列的值并计算代价函数，直到收敛。