尊重原创转载请注明:From AigeStudio(http://blog.csdn.net/aigestudio)Power by Aige 侵权必究!
炮兵 镇楼
镇楼
上1节我们通过引入折线实现了页面的折叠翻转效果,有了前面两节的基础呢其实曲线的实现可以变得非常简单,为何这么说呢?由于曲线不过就是在折线的基础上对Path加入了曲线的实现,进而只是影响了我们的Region区域,而其他的甚么事件啊、滑动计算啊之类的几近都是不变的对吧,说白了就是对现有的折线View进行update改造,虽然是改造,但是我们该如何下手呢?首先我们来看看现实中翻页的效果应当是怎样的呢?如果大家身旁有书或本子乃至1张纸也行,尝试以不同的方式去翻动它,你会发现除我们前面两节曾提到过的1些限制外,还有1些special的现象:
1、翻起来的区域从侧面来看是1个有弧度的区域,如图所示侧面图:
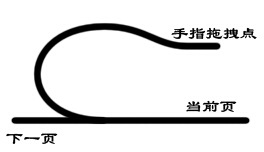
而我们将依照第1节中的约定疏忽这部份弧度的表现,由于从正俯视的角度我们压根看不到弧度的效果,So~我们强迫让其与页面平行:
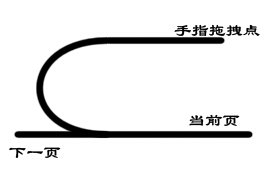
2、根据拖拽点距离页面高度的不同,我们可以得到不同的卷曲度:

而其在我们正俯视点的表现则是曲线的弧度不同:
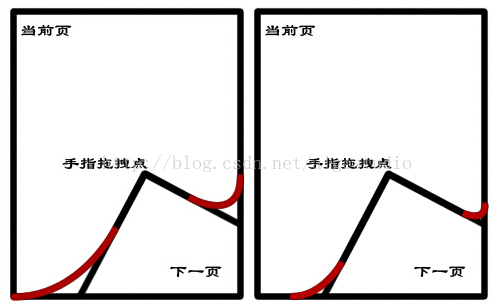
一样的,我们依照第1节的约定,为了简化问题,我们将拖拽点距离页面的高度视为1个定值使在我们正俯视点表现的曲线出发点从距离控件交点1/4处开始:

3、如上1节末所说,在曲折的区域图象也会有相似的扭曲效果
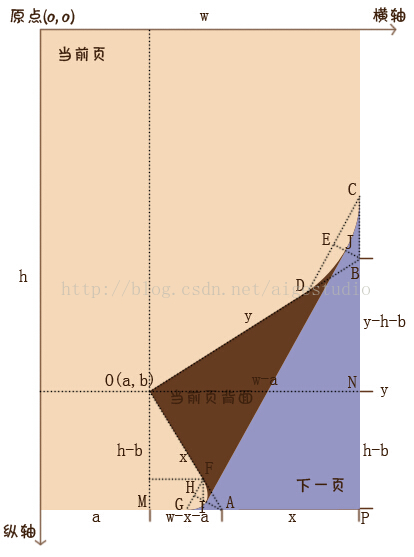
OK,大致的1个分析就是这样,我们根据分析结果可以得出下面的1个分析图:
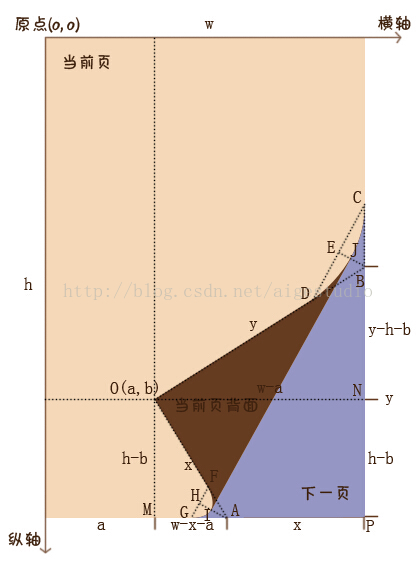
由上图配合我们上面的分析我们可知:DB = 1/4OB,FA = 1/4OA,而点F和点D分别为两条曲线(如无特殊声明,我们所说的曲线均为贝赛尔曲线,下同)的出发点(固然你也能够说是终点无所谓),这时候,我们以点A、B为曲线的控制点并以其为端点分别沿着x轴和y轴方向作线段AG、BC,另AG = AF、BC = BD,并令点G、C分别为曲线的终点,这样,我们的这两条2阶贝塞尔曲线就非常非常的特殊,例如上图中的曲线DC,它是由起始点D、C和控制点B构成,而BD = BC,也就是说3角形BDC是的等腰3角形,进1步地说就是曲线DC的两条控制杆力臂相等,进1步地我们可以推断出曲线DC的顶点J一定在直线DC的中垂线上,更进1步地我们可以根据《自定义控件其实很简单5/12》所说的2阶贝塞尔曲线公式得出当且仅当t
= 0.5时曲线的端点恰好会在顶点J上,由此我们可以非常非常简单地得到曲线的顶点坐标。好了,YY归YY我们还是要回归到具体的操作中来,首先,我们要计算出点G、F、D、C的坐标值,这4点坐标也相当easy,就拿F点坐标来讲,我们过点F分别作OM、AM的垂线:
由于FA = 1/4OA,那末我们可以得到F点的x坐标Fx = a + 3/4MA,y坐标Fy = b + 3/4OM,而G点的x坐标Gx = a + MA - 1/4x;其他两点D、C就不多扯了,那末在代码中如何体现呢?首先,为了便于视察效果,我们先注释掉图片的绘制:
/*
* 如果坐标点在原点(即还没产生触碰时)则绘制第1页
*/
if (mPointX == 0 && mPointY == 0) {
// canvas.drawBitmap(mBitmaps.get(mBitmaps.size() - 1), 0, 0, null);
return;
}
// 省略大量代码
//drawBitmaps(canvas);
并绘制线条:
canvas.drawPath(mPath, mPaint);
在上1节中我们在生成Path时将情况分为了两种:
if (sizeLong > mViewHeight) {
//…………………………
} else {
//…………………………
}
一样,我们也分开处理两种情况,那末针对sizeLong > mViewHeight的时候此时控件顶部的曲线效果已是看不到了,我们只需斟酌底部的曲线效果:
// 计算曲线出发点
float startXBtm = btmX2 - CURVATURE * sizeShort;
float startYBtm = mViewHeight;
// 计算曲线终点
float endXBtm = mPointX + (1 - CURVATURE) * (tempAM);
float endYBtm = mPointY + (1 - CURVATURE) * mL;
// 计算曲线控制点
float controlXBtm = btmX2;
float controlYBtm = mViewHeight;
// 计算曲线顶点
float bezierPeakXBtm = 0.25F * startXBtm + 0.5F * controlXBtm + 0.25F * endXBtm;
float bezierPeakYBtm = 0.25F * startYBtm + 0.5F * controlYBtm + 0.25F * endYBtm;
/*
* 生成带曲线的4边形路径
*/
mPath.moveTo(startXBtm, startYBtm);
mPath.quadTo(controlXBtm, controlYBtm, endXBtm, endYBtm);
mPath.lineTo(mPointX, mPointY);
mPath.lineTo(topX1, 0);
mPath.lineTo(topX2, 0);
mPath.lineTo(bezierPeakXBtm, bezierPeakYBtm);
该部份的实际效果以下:
PS:为了便于大家对参数的理解,我对每个点的坐标都重新给予了1个援用其命名也浅显易懂,实际进程可以省略这1步简化代码
而当sizeLong <= mViewHeight时这时候候不但底部有曲线效果,右边也有:
/*
* 计算参数
*/
float leftY = mViewHeight - sizeLong;
float btmX = mViewWidth - sizeShort;
// 计算曲线出发点
float startXBtm = btmX - CURVATURE * sizeShort;
float startYBtm = mViewHeight;
float startXLeft = mViewWidth;
float startYLeft = leftY - CURVATURE * sizeLong;
/*
* 限制左边曲线出发点
*/
if (startYLeft <= 0) {
startYLeft = 0;
}
/*
* 限制右边曲线出发点
*/
if (startXBtm <= 0) {
startXBtm = 0;
}
// 计算曲线终点
float endXBtm = mPointX + (1 - CURVATURE) * (tempAM);
float endYBtm = mPointY + (1 - CURVATURE) * mL;
float endXLeft = mPointX + (1 - CURVATURE) * mK;
float endYLeft = mPointY - (1 - CURVATURE) * (sizeLong - mL);
// 计算曲线控制点
float controlXBtm = btmX;
float controlYBtm = mViewHeight;
float controlXLeft = mViewWidth;
float controlYLeft = leftY;
// 计算曲线顶点
float bezierPeakXBtm = 0.25F * startXBtm + 0.5F * controlXBtm + 0.25F * endXBtm;
float bezierPeakYBtm = 0.25F * startYBtm + 0.5F * controlYBtm + 0.25F * endYBtm;
float bezierPeakXLeft = 0.25F * startXLeft + 0.5F * controlXLeft + 0.25F * endXLeft;
float bezierPeakYLeft = 0.25F * startYLeft + 0.5F * controlYLeft + 0.25F * endYLeft;
/*
* 生成带曲线的3角形路径
*/
mPath.moveTo(startXBtm, startYBtm);
mPath.quadTo(controlXBtm, controlYBtm, endXBtm, endYBtm);
mPath.lineTo(mPointX, mPointY);
mPath.lineTo(endXLeft, endYLeft);
mPath.quadTo(controlXLeft, controlYLeft, startXLeft, startYLeft);
效果以下:
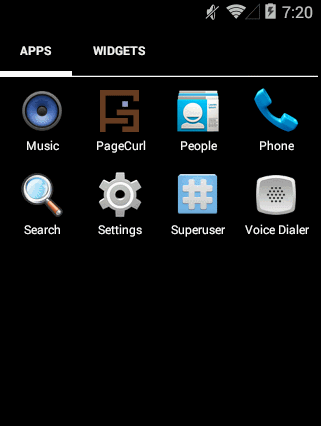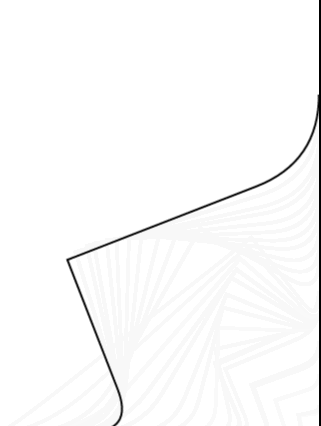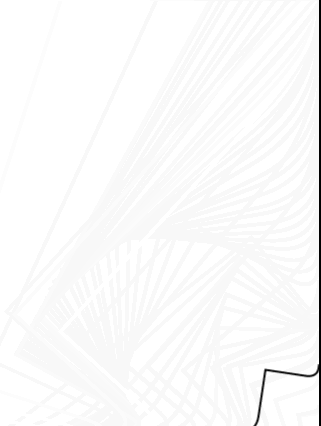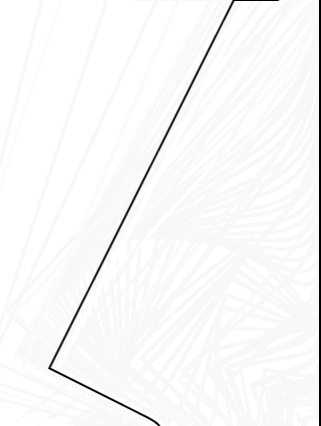
Path有了,我们就该斟酌如何将其转换为Region,在这个进程中呢又1个问题,曲线路径不像上1节的直线路径我们可以轻易取得其范围区域,由于我们的折叠区域其实应当是这样的:

如图所示红色路径区域,这部份区域则是我们折叠的区域,而事实上我们为了计算方便将整条2阶贝赛尔曲线都绘制了出来,也就是说我们的Path除红色线条部份还包括了蓝色线条部份对吧,那末问题来了,如何将这两部份“做掉”呢?其实方法很多,我们可以在计算的时候就只生成半条曲线,这是方法1我们利用纯计算的方式,记得我在该系列文章开头曾说过翻页效果的实现可以有两种方式,1种是纯计算而另外一种则是利用图形的组合思想,如何组合呢?这里对区域的计算我们就不用纯计算的方式了,我们尝试用图形组合来试试。首先我们将Path转为Region看看是甚么样的:
Region region = computeRegion(mPath);
canvas.clipRegion(region);
canvas.drawColor(Color.RED);
// canvas.drawPath(mPath, mPaint);
效果以下:

可以看到我们没有封闭的Path构成的Region效果,事实呢跟我们需要的区域差距有点大,首先上下两个月半圆是过剩的,其次目测少了1块对吧:

如上图蓝色的那块,那末我们该如何把这块“补”回来呢?利用图形组合的思想,我们想法为该Region补1块矩形:

然后差集掉两个月半圆不就成了?这部份代码改动较大,我先贴代码再说吧:
if (sizeLong > mViewHeight) {
// 计算……额……按图来AN边~
float an = sizeLong - mViewHeight;
// 3角形AMN的MN边
float largerTrianShortSize = an / (sizeLong - (mViewHeight - mPointY)) * (mViewWidth - mPointX);
// 3角形AQN的QN边
float smallTrianShortSize = an / sizeLong * sizeShort;
/*
* 计算参数
*/
float topX1 = mViewWidth - largerTrianShortSize;
float topX2 = mViewWidth - smallTrianShortSize;
float btmX2 = mViewWidth - sizeShort;
// 计算曲线出发点
float startXBtm = btmX2 - CURVATURE * sizeShort;
float startYBtm = mViewHeight;
// 计算曲线终点
float endXBtm = mPointX + (1 - CURVATURE) * (tempAM);
float endYBtm = mPointY + (1 - CURVATURE) * mL;
// 计算曲线控制点
float controlXBtm = btmX2;
float controlYBtm = mViewHeight;
// 计算曲线顶点
float bezierPeakXBtm = 0.25F * startXBtm + 0.5F * controlXBtm + 0.25F * endXBtm;
float bezierPeakYBtm = 0.25F * startYBtm + 0.5F * controlYBtm + 0.25F * endYBtm;
/*
* 生成带曲线的4边形路径
*/
mPath.moveTo(startXBtm, startYBtm);
mPath.quadTo(controlXBtm, controlYBtm, endXBtm, endYBtm);
mPath.lineTo(mPointX, mPointY);
mPath.lineTo(topX1, 0);
mPath.lineTo(topX2, 0);
/*
* 替补区域Path
*/
mPathTrap.moveTo(startXBtm, startYBtm);
mPathTrap.lineTo(topX2, 0);
mPathTrap.lineTo(bezierPeakXBtm, bezierPeakYBtm);
mPathTrap.close();
/*
* 底部月半圆Path
*/
mPathSemicircleBtm.moveTo(startXBtm, startYBtm);
mPathSemicircleBtm.quadTo(controlXBtm, controlYBtm, endXBtm, endYBtm);
mPathSemicircleBtm.close();
/*
* 生成包括折叠和下1页的路径
*/
//暂时没用省略掉
// 计算月半圆区域
mRegionSemicircle = computeRegion(mPathSemicircleBtm);
} else {
/*
* 计算参数
*/
float leftY = mViewHeight - sizeLong;
float btmX = mViewWidth - sizeShort;
// 计算曲线出发点
float startXBtm = btmX - CURVATURE * sizeShort;
float startYBtm = mViewHeight;
float startXLeft = mViewWidth;
float startYLeft = leftY - CURVATURE * sizeLong;
// 计算曲线终点
float endXBtm = mPointX + (1 - CURVATURE) * (tempAM);
float endYBtm = mPointY + (1 - CURVATURE) * mL;
float endXLeft = mPointX + (1 - CURVATURE) * mK;
float endYLeft = mPointY - (1 - CURVATURE) * (sizeLong - mL);
// 计算曲线控制点
float controlXBtm = btmX;
float controlYBtm = mViewHeight;
float controlXLeft = mViewWidth;
float controlYLeft = leftY;
// 计算曲线顶点
float bezierPeakXBtm = 0.25F * startXBtm + 0.5F * controlXBtm + 0.25F * endXBtm;
float bezierPeakYBtm = 0.25F * startYBtm + 0.5F * controlYBtm + 0.25F * endYBtm;
float bezierPeakXLeft = 0.25F * startXLeft + 0.5F * controlXLeft + 0.25F * endXLeft;
float bezierPeakYLeft = 0.25F * startYLeft + 0.5F * controlYLeft + 0.25F * endYLeft;
/*
* 限制右边曲线出发点
*/
if (startYLeft <= 0) {
startYLeft = 0;
}
/*
* 限制底部左边曲线出发点
*/
if (startXBtm <= 0) {
startXBtm = 0;
}
/*
* 根据底部左边限制点重新计算贝塞尔曲线顶点坐标
*/
float partOfShortLength = CURVATURE * sizeShort;
if (btmX >= -mValueAdded && btmX <= partOfShortLength - mValueAdded) {
float f = btmX / partOfShortLength;
float t = 0.5F * f;
float bezierPeakTemp = 1 - t;
float bezierPeakTemp1 = bezierPeakTemp * bezierPeakTemp;
float bezierPeakTemp2 = 2 * t * bezierPeakTemp;
float bezierPeakTemp3 = t * t;
bezierPeakXBtm = bezierPeakTemp1 * startXBtm + bezierPeakTemp2 * controlXBtm + bezierPeakTemp3 * endXBtm;
bezierPeakYBtm = bezierPeakTemp1 * startYBtm + bezierPeakTemp2 * controlYBtm + bezierPeakTemp3 * endYBtm;
}
/*
* 根据右边限制点重新计算贝塞尔曲线顶点坐标
*/
float partOfLongLength = CURVATURE * sizeLong;
if (leftY >= -mValueAdded && leftY <= partOfLongLength - mValueAdded) {
float f = leftY / partOfLongLength;
float t = 0.5F * f;
float bezierPeakTemp = 1 - t;
float bezierPeakTemp1 = bezierPeakTemp * bezierPeakTemp;
float bezierPeakTemp2 = 2 * t * bezierPeakTemp;
float bezierPeakTemp3 = t * t;
bezierPeakXLeft = bezierPeakTemp1 * startXLeft + bezierPeakTemp2 * controlXLeft + bezierPeakTemp3 * endXLeft;
bezierPeakYLeft = bezierPeakTemp1 * startYLeft + bezierPeakTemp2 * controlYLeft + bezierPeakTemp3 * endYLeft;
}
/*
* 替补区域Path
*/
mPathTrap.moveTo(startXBtm, startYBtm);
mPathTrap.lineTo(startXLeft, startYLeft);
mPathTrap.lineTo(bezierPeakXLeft, bezierPeakYLeft);
mPathTrap.lineTo(bezierPeakXBtm, bezierPeakYBtm);
mPathTrap.close();
/*
* 生成带曲线的3角形路径
*/
mPath.moveTo(startXBtm, startYBtm);
mPath.quadTo(controlXBtm, controlYBtm, endXBtm, endYBtm);
mPath.lineTo(mPointX, mPointY);
mPath.lineTo(endXLeft, endYLeft);
mPath.quadTo(controlXLeft, controlYLeft, startXLeft, startYLeft);
/*
* 生成底部月半圆的Path
*/
mPathSemicircleBtm.moveTo(startXBtm, startYBtm);
mPathSemicircleBtm.quadTo(controlXBtm, controlYBtm, endXBtm, endYBtm);
mPathSemicircleBtm.close();
/*
* 生成右边月半圆的Path
*/
mPathSemicircleLeft.moveTo(endXLeft, endYLeft);
mPathSemicircleLeft.quadTo(controlXLeft, controlYLeft, startXLeft, startYLeft);
mPathSemicircleLeft.close();
/*
* 生成包括折叠和下1页的路径
*/
//暂时没用省略掉
/*
* 计算底部和右边两月半圆区域
*/
Region regionSemicircleBtm = computeRegion(mPathSemicircleBtm);
Region regionSemicircleLeft = computeRegion(mPathSemicircleLeft);
// 合并两月半圆区域
mRegionSemicircle.op(regionSemicircleBtm, regionSemicircleLeft, Region.Op.UNION);
}
// 根据Path生成的折叠区域
Region regioFlod = computeRegion(mPath);
// 替补区域
Region regionTrap = computeRegion(mPathTrap);
// 令折叠区域与替补区域相加
regioFlod.op(regionTrap, Region.Op.UNION);
// 从相加后的区域中剔除掉月半圆的区域取得终究折叠区域
regioFlod.op(mRegionSemicircle, Region.Op.DIFFERENCE);
/*
* 根据裁剪区域填充画布
*/
canvas.clipRegion(regioFlod);
canvas.drawColor(Color.RED);
200行的代码我们就做了1件事就是正确计算Path,一样我们还是依照之前的分了两种情况来计算,第1种情况sizeLong > mViewHeight时,我们先计算替补的这块区域:

如上代码46⑷9行
/*
* 替补区域Path
*/
mPathTrap.moveTo(startXBtm, startYBtm);
mPathTrap.lineTo(topX2, 0);
mPathTrap.lineTo(bezierPeakXBtm, bezierPeakYBtm);
mPathTrap.close();
然后计算底部的月半圆Path:
对应代码54⑸6行
/*
* 底部月半圆Path
*/
mPathSemicircleBtm.moveTo(startXBtm, startYBtm);
mPathSemicircleBtm.quadTo(controlXBtm, controlYBtm, endXBtm, endYBtm);
mPathSemicircleBtm.close();
将当前折叠区域和替补区域相加再减去月半圆Path区域我们就能够得到正确的折叠区域,对应代码64行和192⑵01行:
// 计算月半圆区域
mRegionSemicircle = computeRegion(mPathSemicircleBtm);
// ………………中间省略巨量代码………………
// 根据Path生成的折叠区域
Region regioFlod = computeRegion(mPath);
// 替补区域
Region regionTrap = computeRegion(mPathTrap);
// 令折叠区域与替补区域相加
regioFlod.op(regionTrap, Region.Op.UNION);
// 从相加后的区域中剔除掉月半圆的区域取得终究折叠区域
regioFlod.op(mRegionSemicircle, Region.Op.DIFFERENCE);
该情况下我们的折叠区域是酱紫的:

两1种情况则略微复杂些,除要计算底部,我们还要计算右边的月半圆Path区域,代码165⑴74:
/*
* 生成底部月半圆的Path
*/
mPathSemicircleBtm.moveTo(startXBtm, startYBtm);
mPathSemicircleBtm.quadTo(controlXBtm, controlYBtm, endXBtm, endYBtm);
mPathSemicircleBtm.close();
/*
* 生成右边月半圆的Path
*/
mPathSemicircleLeft.moveTo(endXLeft, endYLeft);
mPathSemicircleLeft.quadTo(controlXLeft, controlYLeft, startXLeft, startYLeft);
mPathSemicircleLeft.close();
替补区域的计算,147⑴51:
/*
* 替补区域Path
*/
mPathTrap.moveTo(startXBtm, startYBtm);
mPathTrap.lineTo(startXLeft, startYLeft);
mPathTrap.lineTo(bezierPeakXLeft, bezierPeakYLeft);
mPathTrap.lineTo(bezierPeakXBtm, bezierPeakYBtm);
mPathTrap.close();
区域的转换,184⑴88:
/*
* 计算底部和右边两月半圆区域
*/
Region regionSemicircleBtm = computeRegion(mPathSemicircleBtm);
Region regionSemicircleLeft = computeRegion(mPathSemicircleLeft);
// 合并两月半圆区域
mRegionSemicircle.op(regionSemicircleBtm, regionSemicircleLeft, Region.Op.UNION);
终究的计算跟上面第1种情况1样,效果以下:

结合两种情况,我们可以得到下面的效果:
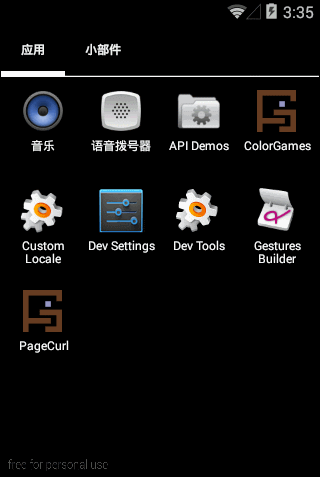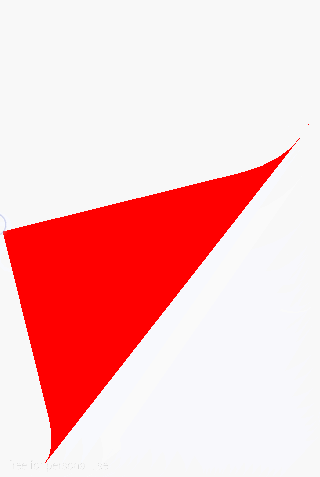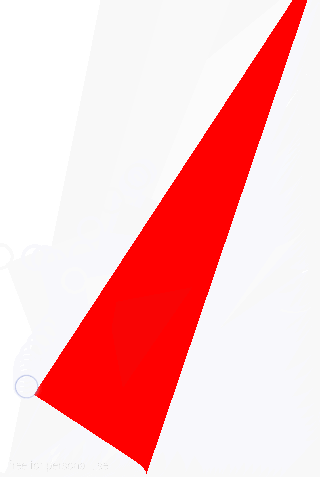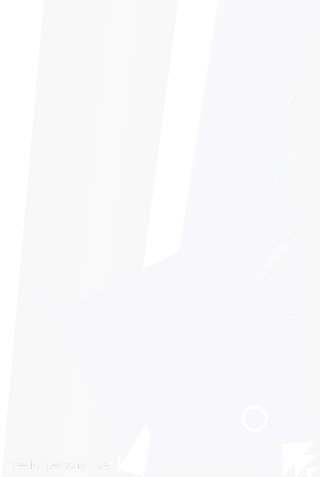
然后,我们需要计算“下1页”的区域,一样,根据上1节我们的讲授,我们先获得折叠区域和下1页区域之和再减去折叠区域就能够得到下1页的区域:
mRegionNext = computeRegion(mPathFoldAndNext);
mRegionNext.op(mRegionFold, Region.Op.DIFFERENCE);
绘制效果以下:
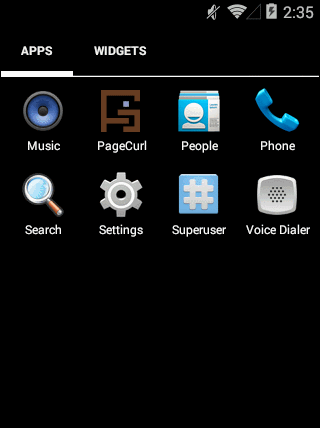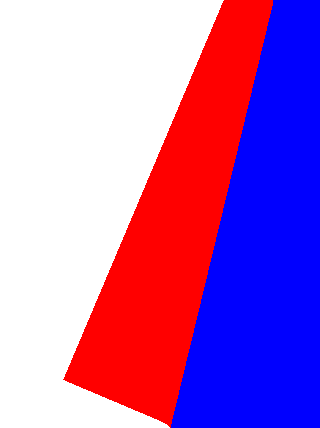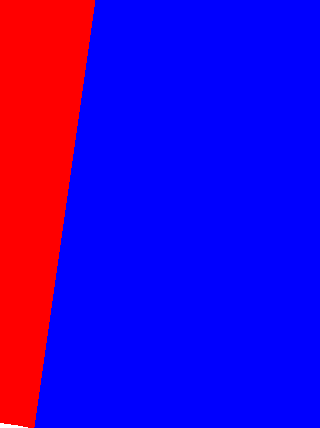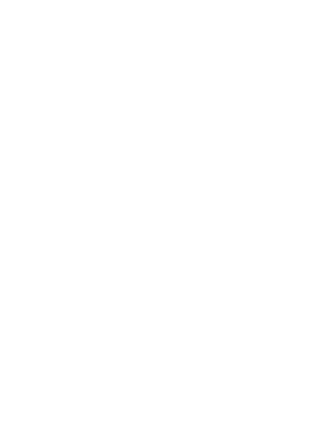
最后,我们结合上两节,注入数据:
/**
* 绘制位图数据
*
* @param canvas
* 画布对象
*/
private void drawBitmaps(Canvas canvas) {
// 绘制位图前重置isLastPage为false
isLastPage = false;
// 限制pageIndex的值范围
mPageIndex = mPageIndex < 0 ? 0 : mPageIndex;
mPageIndex = mPageIndex > mBitmaps.size() ? mBitmaps.size() : mPageIndex;
// 计算数据起始位置
int start = mBitmaps.size() - 2 - mPageIndex;
int end = mBitmaps.size() - mPageIndex;
/*
* 如果数据出发点位置小于0则表示当前已到了最后1张图片
*/
if (start < 0) {
// 此时设置isLastPage为true
isLastPage = true;
// 并显示提示信息
showToast("This is fucking lastest page");
// 强迫重置起始位置
start = 0;
end = 1;
}
/*
* 计算当前页的区域
*/
canvas.save();
canvas.clipRegion(mRegionCurrent);
canvas.drawBitmap(mBitmaps.get(end - 1), 0, 0, null);
canvas.restore();
/*
* 计算折叠页的区域
*/
canvas.save();
canvas.clipRegion(mRegionFold);
canvas.translate(mPointX, mPointY);
/*
* 根据长短边标识计算折叠区域图象
*/
if (mRatio == Ratio.SHORT) {
canvas.rotate(90 - mDegrees);
canvas.translate(0, -mViewHeight);
canvas.scale(⑴, 1);
canvas.translate(-mViewWidth, 0);
} else {
canvas.rotate(-(90 - mDegrees));
canvas.translate(-mViewWidth, 0);
canvas.scale(1, ⑴);
canvas.translate(0, -mViewHeight);
}
canvas.drawBitmap(mBitmaps.get(end - 1), 0, 0, null);
canvas.restore();
/*
* 计算下1页的区域
*/
canvas.save();
canvas.clipRegion(mRegionNext);
canvas.drawBitmap(mBitmaps.get(start), 0, 0, null);
canvas.restore();
}
终究效果以下:
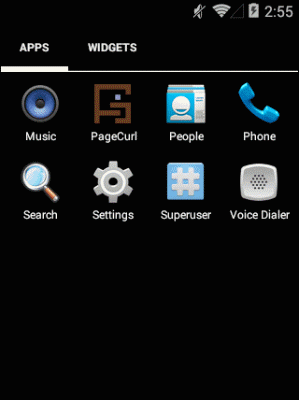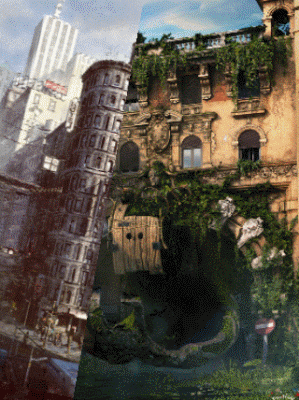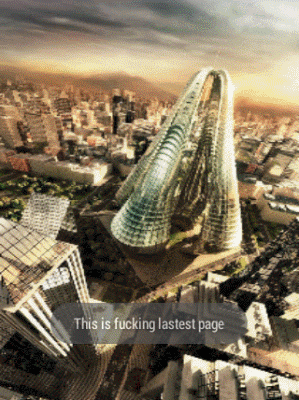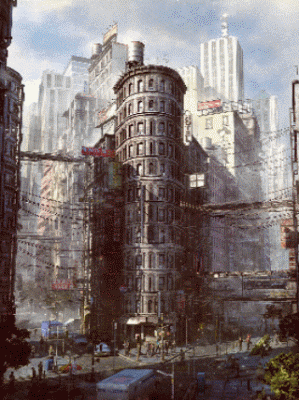
该部份的代码就不贴出了,大部份跟上1节相同,由于过两天要去旅游时间略紧这节略讲得粗糙,不过也没甚么太大的改动,如果大家有不懂的地方可以留言或群里@哥,下1节我们将尝试实现翻页时图象扭曲的效果。
源码地址:传送门
 镇楼
镇楼


















