Cocos2dx CrazyTetris 双线伪裁剪算面积 对于判断消除的思考(二)
栏目:综合技术时间:2015-01-05 08:19:23
上1篇主要讲了我对裁剪消除算法的思考,这1篇的主题是计算单行覆盖面积,以此来肯定是不是到达了裁剪条件。
就像之前所说的,在该游戏中,基本方块都由4个小方块构成,4个小方块的尺寸均是25*25。因此游戏区域是宽可容纳10个方块,高可容纳20个方块。即250*500。每行的间距均是25。
因此,现在的问题就是,如何判定在这个宽250,高25的区域内,方块所占的面积。如果能够计算出其面积,而这个区域的总面积为250 * 25 = 6250,那末就能够据此来判断是不是满足消除条件。例如:面积 > 6000。
因此这里主要是讨论该套面积应当如何计算。
直接接上1篇。上1篇利用裁剪线将图形集合上下切割,而这里明显是要使用两条线,将图形进行上、中、下3片切割,然后根据切割结果计算中部的面积。如图:
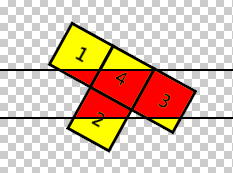
其中红色区域就是要计算的面积。
这时候,算法思想和单线裁剪还是很类似的。这里由于分了3层,因此3层编码需要两位:上层(01)、中层(00)、下层(10)。
然后根据该编码进行裁剪,只保存中部裁剪结果,然后利用裁剪结果(点集)创建PhysicsShapePolygon对象,并用其getArea()方法获得面积便可。
这其中,虽然进行了裁剪算法,但是并没有真正实行裁剪,因此叫做伪裁剪算法。
实现代码以下:
//计算面积算法
float BaseBlock::calculaArea(float y1, float y2)
{
//定义上下多边形集
float area = 0;
//
for(int i=0; i<shapeAmount; i++)
{
//
std::vector<Vec2> * middleShape;
middleShape = new std::vector<Vec2>();
//逐边裁剪
for(int j=0; j<shapeVecAmount->at(i); j++)
{
Vec2 startPoint = this->coordinateSpin(shapeVecs->at(i)[j]);
Vec2 endPoint = this->coordinateSpin(shapeVecs->at(i)[(j+1)%shapeVecAmount->at(i)]);
int cStart = 0;
int cEnd = 0;
//
if((fabs(startPoint.y - y1) < 1e⑹) && (fabs(endPoint.y - y1) < 1e⑹))
{
cStart = cEnd = 0;
}
else if(fabs(startPoint.y - y1) < 1e⑹)
{
if(endPoint.y - y1 < 1e⑹)
{
cStart |= 2;
cEnd |= 2;
}
}
else if(fabs(endPoint.y - y1) < 1e⑹)
{
if(startPoint.y - y1 < 1e⑹)
{
cStart |= 2;
cEnd |= 2;
}
}
else
{
if(startPoint.y - y1 < 1e⑹) cStart |= 2;
if(endPoint.y - y1 < 1e⑹) cEnd |= 2;
}
//
if((fabs(startPoint.y - y2) < 1e⑹) && (fabs(endPoint.y - y2) < 1e⑹))
{
cStart = cEnd = 0;
}
else if(fabs(startPoint.y - y2) < 1e⑹)
{
if(endPoint.y - y2 > 1e⑹)
{
cStart |= 1;
cEnd |= 1;
}
}
else if(fabs(endPoint.y - y2) < 1e⑹)
{
if(startPoint.y - y2 > 1e⑹)
{
cStart |= 1;
cEnd |= 1;
}
}
else
{
if(startPoint.y - y2 > 1e⑹) cStart |= 1;
if(endPoint.y - y2 > 1e⑹) cEnd |= 1;
}
if(cStart == cEnd)
{
//两顶点在同1边,无需裁剪
if(cStart == 0)
{
//顶点在上边,记录到上边顶点集
middleShape->push_back(coordinateGoBack(startPoint));
}
}
else
{
//两顶点在不同边,需要进行裁剪
if(cStart == 0)
{
float cutting_x;
float cutting_y;
if(cEnd == 1)
{
cutting_x = startPoint.x + (endPoint.x - startPoint.x) * (y2 - startPoint.y) / (endPoint.y - startPoint.y);
cutting_y = y2;
}
else
{
cutting_x = startPoint.x + (endPoint.x - startPoint.x) * (y1 - startPoint.y) / (endPoint.y - startPoint.y);
cutting_y = y1;
}
middleShape->push_back(coordinateGoBack(startPoint));
middleShape->push_back(coordinateGoBack(Vec2(cutting_x, cutting_y)));
}
else
{
float cutting_x;
float cutting_y;
if(cStart == 1)
{
cutting_x = startPoint.x + (endPoint.x - startPoint.x) * (y2 - startPoint.y) / (endPoint.y - startPoint.y);
cutting_y = y2;
}
else
{
cutting_x = startPoint.x + (endPoint.x - startPoint.x) * (y1 - startPoint.y) / (endPoint.y - startPoint.y);
cutting_y = y1;
}
middleShape->push_back(coordinateGoBack(Vec2(cutting_x, cutting_y)));
}
}
}
Vec2 * middleTempShape = new Vec2[middleShape->size()];
for(int index = 0; index < middleShape->size(); index++)
{
middleTempShape[index] = middleShape->at(index);
}
area += PhysicsShapePolygon::create(middleTempShape, middleShape->size())->getArea();
}
return area;
}
------分隔线----------------------------
------分隔线----------------------------