http://blog.csdn.net/pipisorry/article/details/52578631

本文讨论（完备数据的）贝叶斯网的参数估计问题：贝叶斯网的MLE最大似然估计和贝叶斯估计。假定网络结构是固定的，且假定数据集D包括了网络变量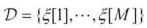的完全观测实例。

参数估计的主要方法有两种：1种基于最大的似然的估计；1种是使用贝叶斯方法。

贝叶斯网的MLE参数估计

最大似然估计MLE

[参数估计：最大似然估计MLE ]

简单示例：局部似然函数

仅包括两个2元变量的网络，即弧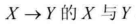

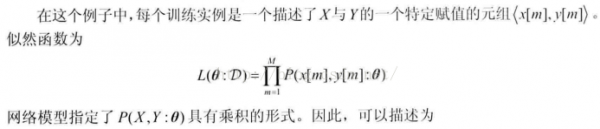
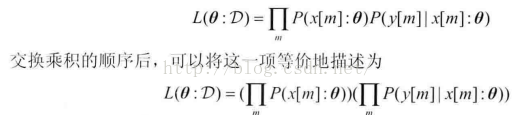
从上看出，似然函数被分解为两项，且每项对应1个变量。每项都是1个局部的似然函数，度量了在给定其父节点时预测变量的性能。每项都只依赖于变量的CPD的参数。

斟酌分解的两个单独项

第1项与前面的多项式似然函数1样。

第2项进1步分解：似然函数的可分解性

局部似然函数分解

同理可得theta y0|x0。但是后面有1个更简单更紧凑的使用CPD表方式快速同时计算这两个参数的方法。

变量集合的各种赋值的计数

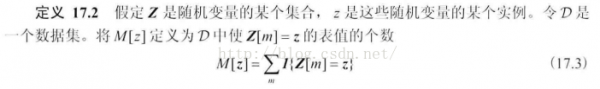
全局似然分解：转换为局部似然函数

注意，贝叶斯网中节点代表的是随机变量（也就是每一个样本的维度，而不是每一个样本）。样本数目为m，维度数为i。

似然函数的全局分解

全局似然分解成局部似然函数乘积

Note: 方括号中的每项表示网络中1个特定变量在给定父节点时的条件似然。

结论

CPD表：进1步分解局部似然函数

参数的选择决定了我们最大化每一个局部似然函数的方法。现斟酌1种多是CPD最简单的参数化：CPD表（table-CPD）。

贝叶斯网局部MLE的进1步分解

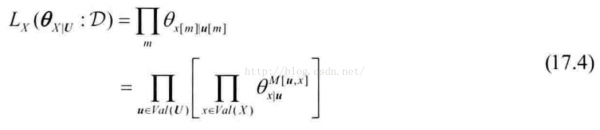
方框项独立最大化

也就是说，之前简单的示例中我们是分别计算p(x0|u0)p(x1|u0)，现在通过式17.5出现次数（更紧凑的表示）1次同时计算出2个参数p(x0|u0)p(x1|u0)了。

Note: 式17.5就是通过MLE估计出的贝叶斯网的参数计算公式。

数据碎片与过拟合：缺少可靠的大量估计参数的数据

高斯贝叶斯网*

。。。

专栏17.B——概念：非参数模型

作为M-投影的最大似然估计*

。。。

皮皮blog

贝叶斯网的贝叶斯参数估计

贝叶斯框架要求在未知的参数和数据实例上指定1个联合散布。与单个参数的情况1样，可以将参数和数据上的联合散布理解为1个贝叶斯网。

贝叶斯参数估计

[参数估计：贝叶斯思想和贝叶斯参数估计 ]

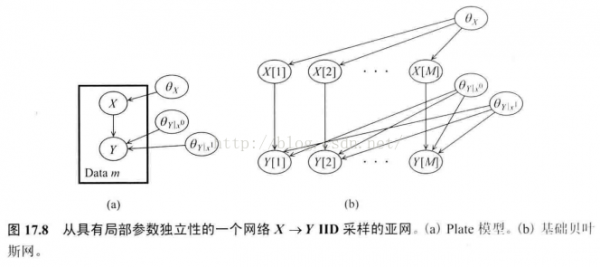
参数独立性与全局分解

简单的例子

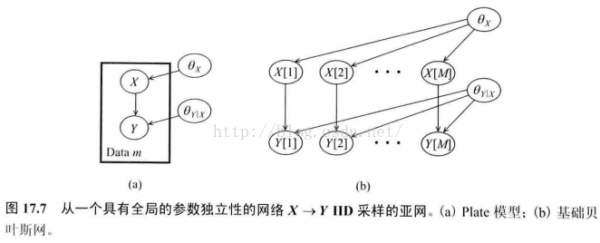
图7中的b

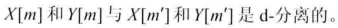
全局参数独立性：假定要估计参数之间独立

这里有1个假定：网络结构体现出单个参数变量的先验是先验独立的（没有观测到数据时就是独立的）。即我们认为知道其中1个参数的参数值其实不能告知我们另外一个参数的任何信息。更确切的有以下定义

同时，如果参数变量是先验独立的，那末观测到数据时，也能够得到它们是后验独立的。也就是说，如果这两个参数是独立的先验，那末它们也是独立的后验。

也就是后验可以用紧凑的因子分解的情势表达。

1般的网络

假定已给定了1个具有参数theta的网络结构G。

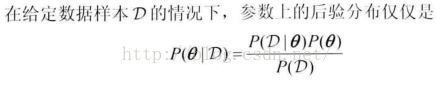
所以，从上面终究的公式中可以看出，这个和MLE很类似，剩下要做的就是先验p(thetax|pax)的肯定上了（其中p(thetax我们已知道了，如Dirichlet散布)）。

预测

局部份解和贝叶斯网学习的先验散布

通过对局部贝叶斯估计问题求解来得到全局贝叶斯解。

theta x的后验

theta y|x的后验

上面独立先验的证明：

theta y|x的狄利克雷散布先验

预测和参数估计

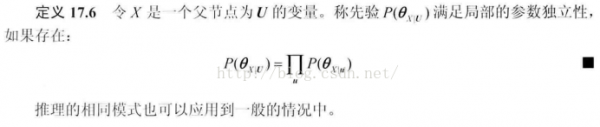
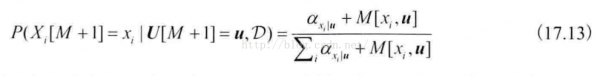
此式应当也就是贝叶斯网的贝叶斯参数估计计算公式。

贝叶斯网学习的先验散布参数的肯定

专家赋值、K2先验（相同的固定先验）、利用先验数据集（等价于MLE了）、BDe先验散布。

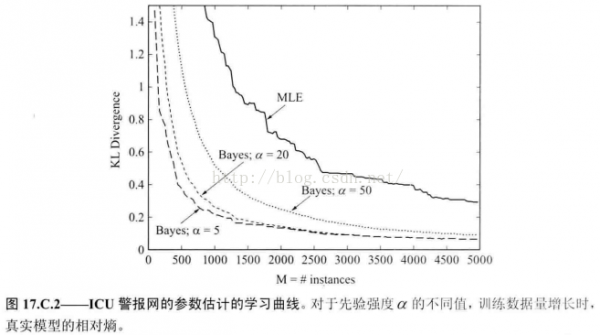
先验对参数估计的影响：MLE和不同强度alpha贝叶斯估计的比较

专栏17.C

检验了MLE方法和1些贝叶斯方法，所有方法使用了统1的先验均值和不同的先验强度alpha。

MAP估计*

。。。[参数估计：文本分析的参数估计方法]

皮皮blog

from: http://blog.csdn.net/pipisorry/article/details/52578631

ref: [《Probabilistic Graphical Models：Principles and Techniques》(简称PGM)]