Andrew Ng Machine Learning 专题【Anomaly Detection】

此文是斯坦福大学，机器学习界 superstar ― Andrew Ng 所开设的 Coursera 课程：Machine Learning 的课程笔记。力求简洁，仅代表本人观点，不足的地方希望大家探讨。
课程网址：https://www.coursera.org/learn/machine-learning/home/welcome

Week 9 后半部份 Recommender Systems：敬请等待

Week 9：

1. 异常检测 & 高斯散布

   1. 异常检测是1种介于监督学习与非监督学习之间的机器学习方式。1般用于检查大范围正品中的小范围次品。根据单个特点量的几率散布，从而求出某个样本正常的几率，若正常的几率小于阈值，即 p(x)<? 视其为异常（次品）。正品与次品的 label 值 y 定义为：
      

      y={01if p(x)≥?if p(x)<?
      
      如果某个样本由x1,x2两个变量决定，以下图红色叉所示：
      
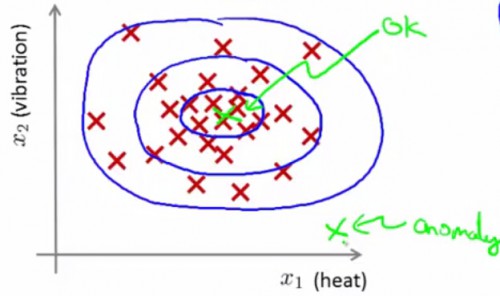
      同1个圆圈内部，表示的是成为正品的几率相同。越中心的圆圈内部正品率越高。越外层的圆圈内正品率越低。

      
      

   2. 异常检测1般将每一个特点量的散布假定为正态散布（如果特点量与正态散布差距很大，以后我们会提到方法对其进行修正）。为何是正态散布？由于在生产与科学实验中发现，很多随机变量的几率散布都可以近似地用正态散布来描写（猜想正确的几率更大）。因此，以下略微介绍1下正态散布的基础知识，如果很熟习的同学可以略过这部份。

   3. 正态散布（高斯散布），包括两个参数：均值μ（散布函数取峰值时所对应横坐标轴的值），与方差σ2（标准差为σ，控制散布函数的“胖瘦”）。如果变量 x 满足于正态散布，将其记为 x～N(μ,σ2)。而取某个 x 的对应正品几率为：p(x)=12π√σe?(x?μ)22σ2

   4. 均值 μ=1m∑i=1mx(i)，方差 σ2=1m∑i=1m(x(i)?μ)2
   5. 正态散布曲线与坐标轴之间的面积（即函数积分）恒定为 1，因此“高”曲线必定“瘦”，“矮”曲线必定“胖”：
      
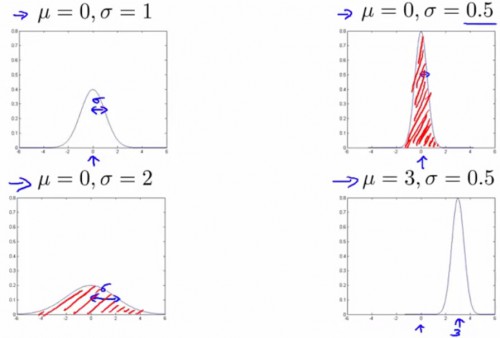
      由图可知，标准差σ控制着散布函数的“胖瘦”。缘由是由于标准差有关的取值范围，有着固定的散布几率（积分）：
      

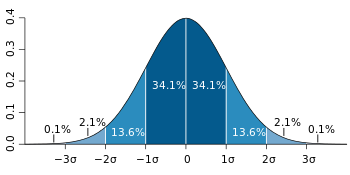
2. 异常检测算法流程：

   1. 我们具有1组训练数据：x(1),x(2),...,x(m)，每一个样本有着 m 个特点量 x1,x2,...,xn
      
      • 将每一个样本投影到不同的特点的坐标轴上，基于样本得到各个特点的几率正态散布曲线
      • 假定各个特点的几率是独立的，因此单个样本的异常几率为
        p(x)=p(x1;μ1,σ21)×p(x2;μ2,σ22)×...×p(xn;μn,σ2n))=∏i=1np(xj;μj,σ2j)
      • 各个特点的均值为 μj=1m∑i=1mx(i)j，方差为 σ2j=1m∑i=1m(x(i)j?μj)2
   2. 如果我们有着 10000 个正品样本，和 20 个次品样本，我们应当这样辨别训练集、交叉验证集，与测试集：
      
      • 训练集：6000个正品作为训练集（不包括次品样本）
      • 交叉验证集：2000 个正品样本 + 10 个次品样本。用以肯定次品几率的阈值 ?
      • 测试集：2000 个正品样本 + 10 个次品样本。用以判断算法的检测效果
   3. 特别注意，由于使用异常检测的样本集合1般都是偏斜严重的（正品样本远远多于次品样本）。因此，需要在《专题【Machine Learning Advice】》http://blog.csdn.net/ironyoung/article/details/48491237 中提到的 precision/recall/F-score 来进行判断算法的检测效果。

3. 异常检测 VS. 监督学习

   1. 监督学习方法与异常检测类似，处理对象都是1堆有 label 的样本，并且目标都是预测新样本的种别。那末甚么时候使用监督学习的方法？甚么时候使用异常检测的方法？
   2. 大体上，区分以下：
      
      • 样本比例：异常检测适用于正样本（y=1，即次品）个数远远小于负样本的个数的情况；监督学习适用于正负样本个数都非常多的情况
      • 异常规律：如果正样本（y=1，即次品）有着难以预测的模式，引发正样本的缘由有很多很多，适用于异常检测；但是如果正样本有着固定的规律，比如感冒（病因已被研究透彻），可以尝试基于大量的样本使用监督学习的方法建立模式进行判断

4. 特点选择

   1. 绝大多数情况下，特点量符合正态散布的散布情况。但如果特点的散布极端不符合，我们只能对其进行1些处理，以产生全新的特点来适用于异常检测算法。例如：
      
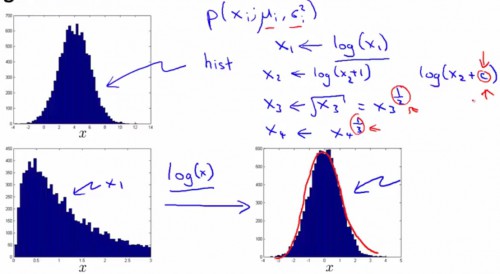
      此时，我们有着变换后的特点变量：xnew=log(x1)
   2. 或，1般情况下我们希望正品的 p(x) 很大，次品的 p(x) 很小。也就是说，在异常情况下某些特点应当变得极大或极小（正态散布中对极大值或极小值的对应几率都是极小的，所以全部样本的正品几率相乘会很容易满足 p(x)<?）：例如创建新变量xnew=x21x2，进1步放大了值增大或减小的程度。

5. Multivariate Gaussion（选学）

   1. 如果1个样本有着多种特点，那末整体的正品几率可以依照以上提到的，视每一个变量为相互独立然后各自几率相乘进行求解（我们称之为 original model）。但是，如果出现了下图这类正相干（负相干）极强的特点量，同心圆内部的正品几率必定不同，明显不适合了：
      
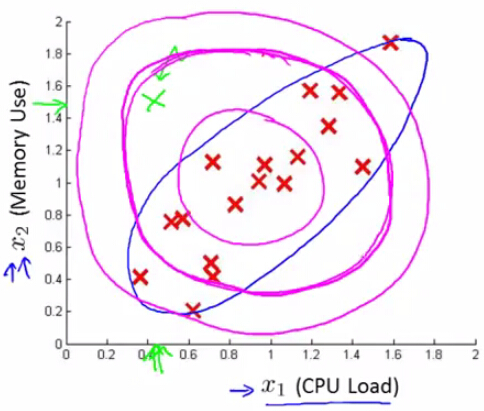
      我们希望本来的同心圆可以更扁，可以变换方向，例如上图的蓝色椭圆。

   2. 此时，我们可以利用协方差矩阵，构造全新的多变量正态散布公式。此时我们用到的不再是方差 σ2，而是协方差矩阵 Σ∈Rn×n：Σ=1m(x(i)?μ)(x(i)?μ)T。多变量正态散布的几率公式为：
      p(x)=1(2π)n/2|Σ|1/2e?12(x?μ)TΣ?1(x?μ)，其中|Σ|表示协方差矩阵的行列式。

   3. 协方差矩阵与均值，对几率散布图的影响以下：
      
      
      
      

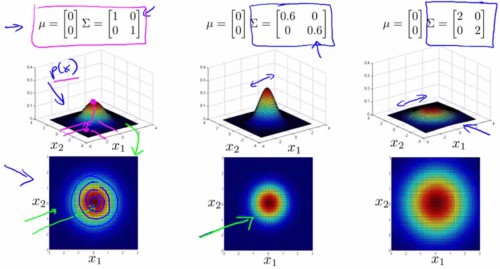
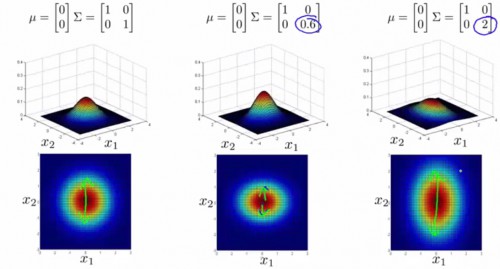
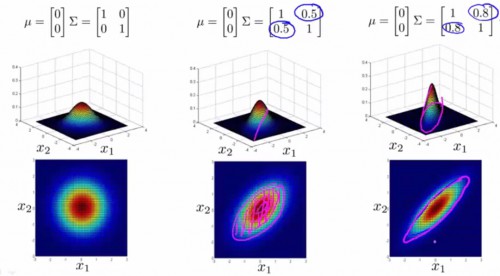
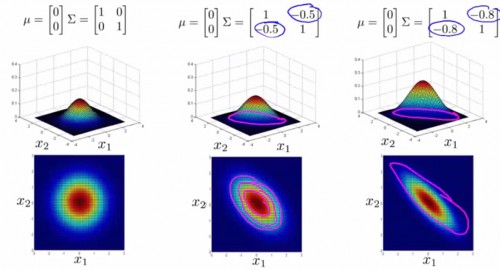
6. original model VS. multivariate Gaussian

   1. 如果1个样本有着多种特点，那我们究竟是应当使用 original model，还是 multivariate Gaussian？
   2. 大体上，区分以下：
      
      • 特点选择：original model 中的各个单个特点（或创造出的新特点），应当尽可能满足在异常情况下产生几率极小的特性；而如果特点之间，发现了正相干或负相干的关系，应当用 multivariate Gaussian
      • 计算效力：original model 仅仅乘法，效力较高；multivariate Gaussian 需要计算协方差的逆矩阵，效力较低
      • 样本数目：original model 在训练集极小的情况下也能够计算；multivariate Gaussian 最少需要训练集样本数目大于特点数目，否则协方差矩阵没法求逆
   3. 协方差矩