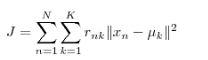鸢尾花数据是1个简易有趣的数据集。这个数据集来源于科学家在1岛上找到1种花的3种不同亚种别,分别叫做setosa,versicolor,virginica。但是这3个种类其实不是很好辩白,所以他们又从花萼长度,花萼宽度,花瓣长度,花瓣宽度这4个角度丈量不同的种类用于定量分析。基于这4个特点,这些数据成了1个多重变量分析的数据集。下面,我们就利用sklearn试着从不同的角度去分析1下这个数据集。
第1种思路是这样:这3种不同的品种每种想必都会有特点或存在1定的相似性。我们无妨先把这些杂乱无章的数据分成3类,然后对应的标出他们每类的种别。如果依照这样的想法,那末这1个问题就变成了1个聚类问题。
作为聚类问题,我们可以用k-means模型去解决。可以参考这1篇博文。网址以下:
http://blog.csdn.net/heavendai/article/details/7029465
首先大体了解1下k-means,这1种算法是非监督模型,也就是说1开始我可以不用告知它种别,让他们自己去分类。那末怎样去分类呢?假定我们首先将它映照到欧式空间
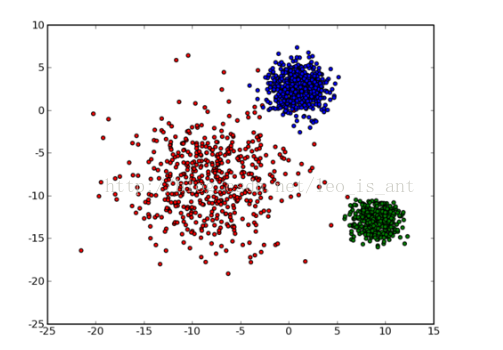
可以直观的看出来,图中把点分成了3类。然后我们做出这样1种假定:每类有1个中心点,这1类的绝大部份点到中心点的距离应当是小于到其他类中心点的距离的。之所以说绝大部份是由于斟酌到点的特例,我们不能由于单独的几个点而否定之前的大部份。基于这1个思想我们可以肯定所要优化的目标函数,我们假定分类N个数据到K个种别,则有:
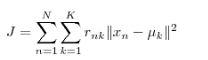
其中的rnk意味着归类到k时为1,剩下为0.剩下的具体如何优化这里不在详细说了。
我们来看实现代码
<span style="font-family:Microsoft YaHei;">from sklearn.cluster import KMeans
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
clf=KMeans(n_clusters=3)
model=clf.fit(X)
predicted=model.predict(X)</span>
这里调用了聚类器KMeans,由于已知3类我们让其中的clusters中心点为3就能够了。
KMeans的参数除聚类个数以外还有max_iter,n_init,init,precompute_distances等。具体的参数含义解释以下网址:
http://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html#sklearn.cluster.KMeans
如果想更加直观1点的话,官网有鸢尾花数据在k-means上的1个demo网址以下:
我们po出代码:
<span style="font-family:Microsoft YaHei;">print(__doc__)
# Code source: Gaël Varoquaux
# Modified for documentation by Jaques Grobler
# License: BSD 3 clause
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.cluster import KMeans
from sklearn import datasets
np.random.seed(5)
centers = [[1, 1], [⑴, ⑴], [1, ⑴]]
iris = datasets.load_iris()
X = iris.data
y = iris.target
estimators = {'k_means_iris_3': KMeans(n_clusters=3),
'k_means_iris_8': KMeans(n_clusters=8),
'k_means_iris_bad_init': KMeans(n_clusters=3, n_init=1,
init='random')}
fignum = 1
for name, est in estimators.items():
fig = plt.figure(fignum, figsize=(4, 3))
plt.clf()
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)
plt.cla()
est.fit(X)
labels = est.labels_
ax.scatter(X[:, 3], X[:, 0], X[:, 2], c=labels.astype(np.float))
ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([])
ax.set_xlabel('Petal width')
ax.set_ylabel('Sepal length')
ax.set_zlabel('Petal length')
fignum = fignum + 1
# Plot the ground truth
fig = plt.figure(fignum, figsize=(4, 3))
plt.clf()
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)
plt.cla()
for name, label in [('Setosa', 0),
('Versicolour', 1),
('Virginica', 2)]:
ax.text3D(X[y == label, 3].mean(),
X[y == label, 0].mean() + 1.5,
X[y == label, 2].mean(), name,
horizontalalignment='center',
bbox=dict(alpha=.5, edgecolor='w', facecolor='w'))
# Reorder the labels to have colors matching the cluster results
y = np.choose(y, [1, 2, 0]).astype(np.float)
ax.scatter(X[:, 3], X[:, 0], X[:, 2], c=y)
ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([])
ax.set_xlabel('Petal width')
ax.set_ylabel('Sepal length')
ax.set_zlabel('Petal length')
plt.show()</span>
这个代码用了很多matplotlib的函数,将不同品种花聚类以后又标定了出来,而且图是3D的可以用鼠标从不同角度视察,效果很炫酷。展现几个效果~

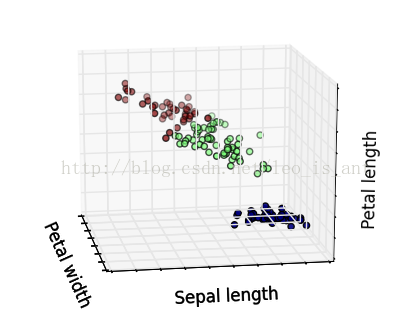
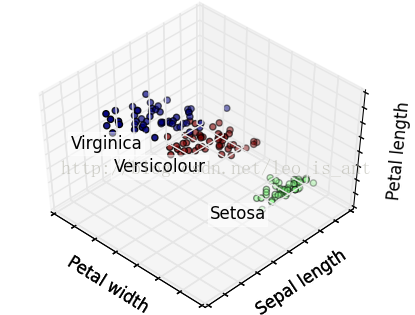
除聚类的思想以外已知了它的种别和数据,我们也能够把它当作1个监督学习的模型来做。这样的话研究的问题就成了1个分类问题。分类问题的模型很多LR,SVM,DT都可以解决。这里用决策树做1个简单的样例。
实现之前简单的了解1下这个模型。可以参考之前的博客
http://blog.csdn.net/leo_is_ant/article/details/43565505
首先决策树是1种树形结构,其中每个内部节点表示1个属性上的测试,每个分支代表1个测试输出,每个叶子节点代表1个种别。这类结构构建在已知各种情况产生几率的基础上,所以我们在构建决策树的时候先要选择能最大程度分离各个属性的特点(即信息增益最大的特点),然后根据分类的情况决定是不是再用剩下的数据集和特点集构建子树。
我们再看1下实现的代码:
<span style="font-family:Microsoft YaHei;">from sklearn.datasets import load_iris
from sklearn.cross_validation import cross_val_score
from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier(random_state=0)
iris = load_iris()
model=clf.fit(iris.data, iris.target)
predicted=model.predict(iris.data)
score=cross_val_score(clf, iris.data, iris.target, cv=10)</span>
这里面,用了决策树的分类器,去做分类。这里注意,由于是监督问题,所以fit方法用时需要 iris.target 这1个变量哟~
最后注意1下cross_val_score这1个方法,是1个交叉验证的手段,原理是将数据分成了cv份,1份来训练剩下的来预测,终究得到的评分能够避免过拟合。
最后给出决策树分类器的参数网址:
http://scikit-learn.org/stable/modules/classes.html#module-sklearn.tree