R语言数据分析系列之7

回归分析建模是数据分析里面很重要的1个利用之1，即通过使用已有的自变量的值建立某种关系，来预测未知变量（因变量）的值。如果因变量是连续的那就是回归分析，如果因变量为离散的，可以理解为是分类。在机器学习算法中，不论是连续变量预测还是离散的变量预测，我们都称之为有监督学习。

回归分析可以用来做广告点击率预测也能够用来做销量预测，app各种指标预测，或库存量，分仓铺货预测等。既然如此奇异，那末我们就来看1下回归是如何做到的。

数据集

我们本节利用women数据集，做1些简单的预测。

1元线性回归分析

输入：1元自变量x，1元因变量y，寻觅y与x的关系，

线性模型假定：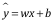

模型误差：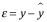

目标：找到参数w和b使得误差平方和最小即

方法：最小2乘法，为了求得w,b使得上式成立，我们可以对参数求偏导数，令偏导数等于零，来求解。

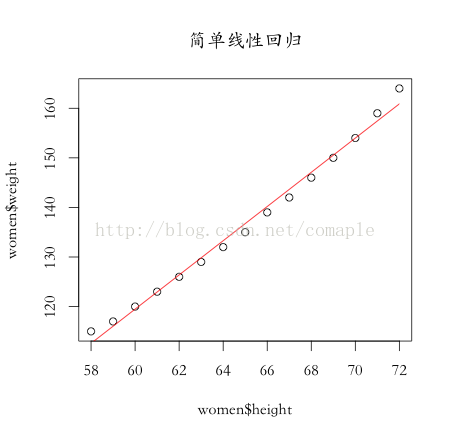
在R语言里面线性回归可以用lm函数来拟合数据集，假设我们要预测女性身高对体重的影响，那末可以建模为简单地线性模型即：weight = w * height + b用R语言来实现很简单以下：

Residuals:

   Min      1Q  Median     3Q     Max

⑴.7333 ⑴.1333 -0.3833  0.7417 3.1167

Coefficients:

            Estimate Std. Error t value Pr(>|t|)   

(Intercept) ⑻7.51667    5.93694 ⑴4.74 1.71e-09 ***

height        3.45000    0.09114  37.85 1.09e⑴4 ***

---

Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’1

Residual standard error: 1.525 on 13degrees of freedom

Multiple R-squared:  0.991,       AdjustedR-squared:  0.9903

F-statistic:  1433 on 1 and 13 DF,  p-value: 1.091e⑴4

在summary的结果中我们可以看到，Intercept截距为b的值，height即为w的值

结果验证：

有了这个模型是不是合适呢，或合适的程度有多大，我们从summary的结果可以分析得到，首先是Residual standard error，值得是预测结果和实际值得残差的均方值即RMSE该值越小证明模型越好，AdjustedR-squared:该值为r方值，也就是自变量与因变量的相干程度，可理解为模型对数据集的解释程度，p-value: 该值为T检验，1般认为<0.005时模型参数通过检验。

我们通过绘图直观的视察1下：

多项式回归分析

输入：多元回归的输入为1个向量，即X是1组变量

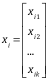
而对应的参数W也应当是1个向量

 回归模型假定为：

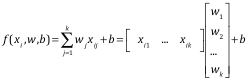
我们可以把模型化简：

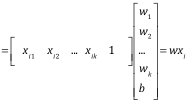
因而模型简化为：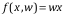

模型误差：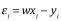

目标：通过学习找到1个向量使得模型误差的平方和最小,即模型的损失函数以下

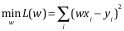
下面我的目标就是要优化这个W向量使得我们的损失函数最小化。我们可以进行矩阵运算，对w求偏导数，并令结果等于0，通过推到整理我们可以得到以下结果：

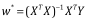
这样我们只通过矩阵运算来求得W向量的值。

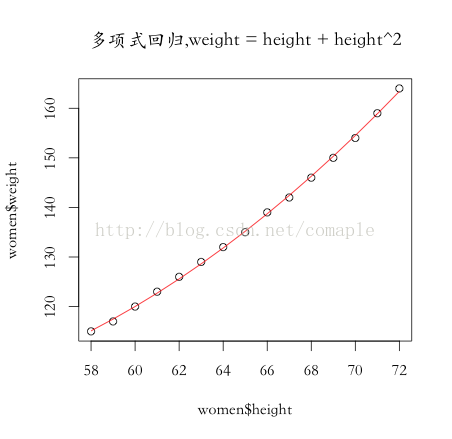
下面基于R来实现1个简单的多远回归，在R中已实现了1个最小2乘法的回归模型，我们1样还是直接调用便可，我们仍然采取women数据集，并将weight变量做平方变换，即模型公式为：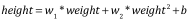

R语言实现：

Call:

lm(formula = weight ~ height + I(height^2),data = women)

Residuals:

    Min       1Q   Median      3Q      Max

-0.50941 -0.29611 -0.00941  0.28615 0.59706

Coefficients:

            Estimate Std. Error t value Pr(>|t|)   

(Intercept) 261.87818   25.19677 10.393 2.36e-07 ***

height      ⑺.34832    0.77769  ⑼.449 6.58e-07 ***

I(height^2)   0.08306   0.00598  13.891 9.32e-09 ***

---

Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’1

Residual standard error: 0.3841 on 12degrees of freedom

Multiple R-squared:  0.9995,     AdjustedR-squared:  0.9994

F-statistic: 1.139e+04 on 2 and 12 DF,  p-value: < 2.2e⑴6

从结果我们可以看出，RMSE减少到0.38残差均方值变小，R方值变大0.999更好的拟合了真是数据，Pr（>|t|）该值是对应参数的T检验，明显小于0.005各参数均通过检验。最后上图以下：