灰度图像--频域滤波 概论
栏目:服务器时间:2015-02-09 09:02:41
学习DIP第25天
转载请标明本文出处:http://blog.csdn.net/tonyshengtan,欢迎大家转载,发现博客被某些论坛转载后,图象没法正常显示,没法正常表达本人观点,对此表示很不满意。有些网站转载了我的博文,很开心的是自己写的东西被更多人看到了,但不开心的是这段话被去掉了,也没标明转载来源,虽然这并没有版权保护,但感觉还是不太好,出于尊重文章作者的劳动,转载请标明出处!!!!
开篇空话
这两天写了1下频域滤波的代码,并且发现之前博客里代码的1个BUG,产生BUG的缘由是1维存储的2维矩阵行宽和列长被写反了,而且测试没有测出来,看来测试是必要的,而且还学习了下使用github,托管代码,由于是小菜,托管HelloWorld也不丢人,频域滤波打算写两到3篇,然后结束,进行下1大块问题的研究。
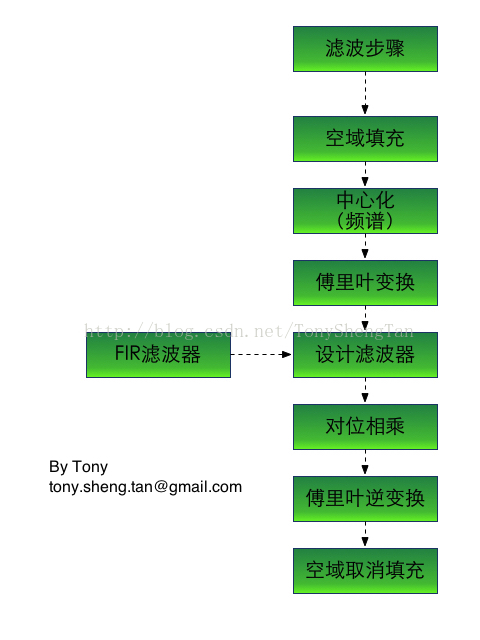
频域滤波的主要知识框架作了1个结构图,完全个人理解,如有理论上的问题,请及时指出:
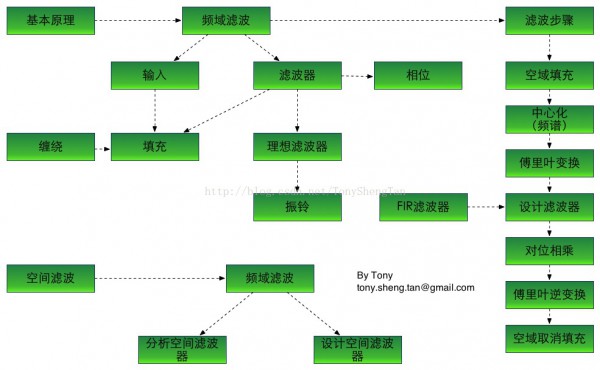
频域滤波基础
对空域滤波和时域滤波,其最重要的理论基础就是,频率域的高频部份对应于空域中变化峻峭的细节,而频域的低频部份对应于空域变化换面的平坦区域,为了得到平滑或峻峭的部份,我们就想到了频域滤波,在空域中对细节和非细节的提取和定义并没有频域那末直接与明确,通过频域这个实验室,可以得出很多针对不同问题,特殊的滤波器,然后将其转换到空域,生成小模板,使用卷积运算来完成快速的滤波,到达我们的目的。基本关系示意图:
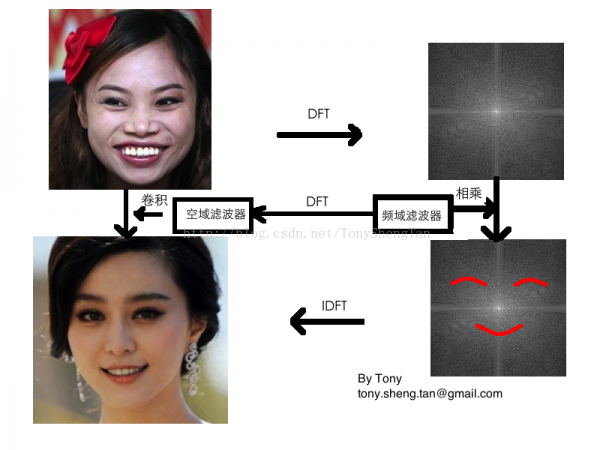
没错,冰冰和凤姐就差1个滤波器!(此为示意图,没有这样的滤波器,请勿模仿0.0)
我们的基本原理就是高频对应变化峻峭的部份,低频对应变化缓慢的部份。低频和高频在频率域以数字度量,滤波器对频域的数字进行不同程度的增强或抑制,以后进行逆变换,得到想要的图象,频域滤波器必须在频域关于原点对称,不然对称部份频率的逆变换将是原图产生伪影效果。
影响频域滤波效果的只有输入和滤波器,对未处理的输入,如果直接进行DFT和滤波的话,会产生纠缠效果,我们来看数学效果:
卷积定理表明:对3x3的两个矩阵a和b的卷积,应当等于a的DFT和b的DFT对位相乘(对位相乘的意思就是对a和b对位相乘的结果c,c(x,y)=a(x,y)*b(x,y),而非1般的矩阵相乘),再进行IDFT变换,就能够得到和空域的卷积结果,但我们得到的结果是:
clear all;clc;
a=[1 2 1;1 1 1 ;0 2 1];
fa=fft2(a);
b=[3 2 1;3 1 1 ;2 0 1];
fb=fft2(b);
temp=eye(3);
for R=1:3
for C=1:3
temp(R,C)=fa(R,C)*fb(R,C);
end
end
res=ifft2(temp);
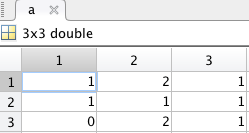 卷积
卷积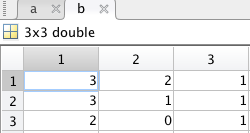 等于结果:
等于结果:
通过我们用手计算,发现结果不对,这是甚么缘由呢,我们暂时不说缘由,我们把矩阵用0扩充到5x5:
clear all;clc;
a=[1 2 1 0 0;1 1 1 0 0;0 2 1 0 0;0 0 0 0 0;0 0 0 0 0];
fa=fft2(a);
b=[3 2 1 0 0;3 1 1 0 0;2 0 1 0 0;0 0 0 0 0;0 0 0 0 0];
fb=fft2(b);
temp=eye(5);
for R=1:5
for C=1:5
temp(R,C)=fa(R,C)*fb(R,C);
end
end
res=ifft2(temp);
 卷积
卷积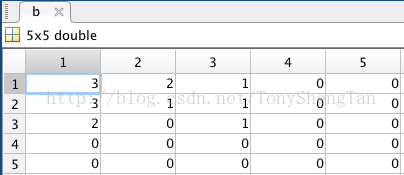 等于
等于
没错,看红色框框,和我们用笔算的3x3的结果1样;
缘由是,如果对1个有限宽度为A的信号使用宽度为B的窗进行卷积,那末结果将会是1个宽度为A+B⑴的信号,但如果信号宽度为A但周期也是A即信号尾部和下1个周期的头是紧挨着的话,那末进行卷积的时候尾部的信号就会和头部的信号相互纠缠,使结果的头部和尾部遭到污染,中间部份保持正确,但如果信号比较短,就像上面3x3的话就完全被污染了。
但上面的信号是其实不是周期的,而是有限宽度的,问题就出在DFT上,由于DFT把信号扩充了,而且是周期性的扩充,DFT时信号实际上是这样的:

所以DFT的两个信号就是周期的而不是我们之前输入的信号,所以就会产生纠缠

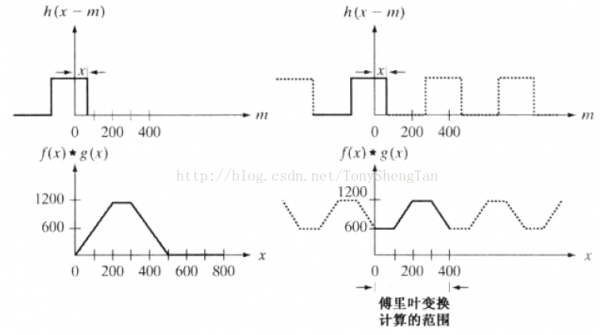
避免这个问题很简单,对两个矩阵都用用0进行填充,填充成5x5后,得到正确的卷积结果。
滤波器的特性,滤波器是对傅里叶谱的实部和虚部进行等比增强或抑制,也就是傅里叶谱经过滤波器后,相位是没有变化的,主要缘由之条件到过,就是1个谱的相角决定了图片的主要结构特点,所以,如果改变相角,那图片将产生巨大问题,所以使用的滤波器都是0相移的,但如果使用非0相移可以得到其他目的的结果,比如让1幅图面目全非。
对理想滤波器,我们必须斟酌其扩充问题,缘由是,离线理想滤波器是频域的,其扩充应当在空域进行,而理想滤波器的IDFT在空域不是有限的而是1个无穷的sinc函数,进行阶段后再填充,返回频率域后填充后的滤波器将产生严重的振铃现象,这里我们的办法是只对图象进行填充,填充到原图的4倍大小,然后使用填充后大小的滤波器,来减轻缠绕问题,同时时使问题简单化,但只是减缓缠绕问题,振铃问题仍然存在。
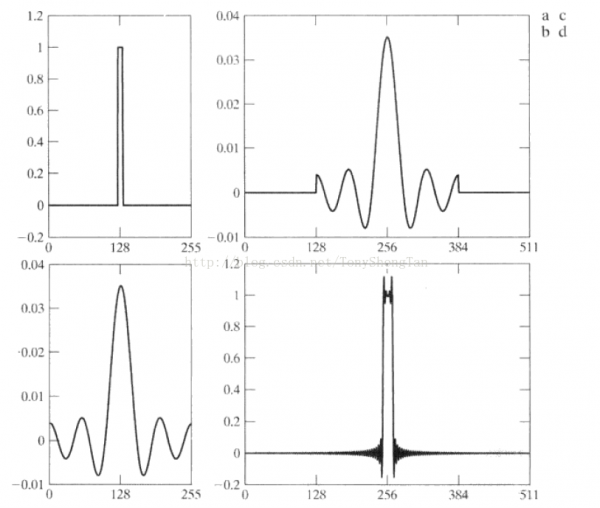
上图a为频率域1维理想滤波器,b为IDFT后的空间波形,c是进行填充,d是填充后DFT的结果
下面我来解释下振铃现象,来个官方的解释:
振铃效应(Ringingeffect)是影响复原图象质量的众多因素之1,其典型表现是在图象灰度剧烈变化的邻域出现类吉布斯(Gibbs)散布--(满足给定束缚条件且熵最大的散布)的振荡。在图象盲复原中,振铃效应是1个不可忽视的问题,其严重下降了复原图象的质量,并且使得难于对复原图象进行后续处理。振铃效应是由于在图象复原当选取了不适当的图象模型酿成的;在图象盲复原中如果点分散函数选择不准确也是引发复原结果产生振铃效应的另外一个缘由,特别是选用的点分散函数尺寸大于真实点分散函数尺寸时,振铃现象更加明显;振铃效应产生的直接缘由是图象退化进程中信息量的丢失,特别是高频信息的丢失。
官方解释可能不好理解,在频域理想滤波器情况下,其实就是sinc函数产生的,只斟酌上图的a和b,a是频域理想滤波器,b就是空域与之对应的滤波器,图象如果和b卷积,结果必定产生类似波浪1样的噪声,图象边沿将会产生抖动,边沿变宽,这就是振铃效果,我们来视察不同截止频率的理想滤波器和其IDFT效果:



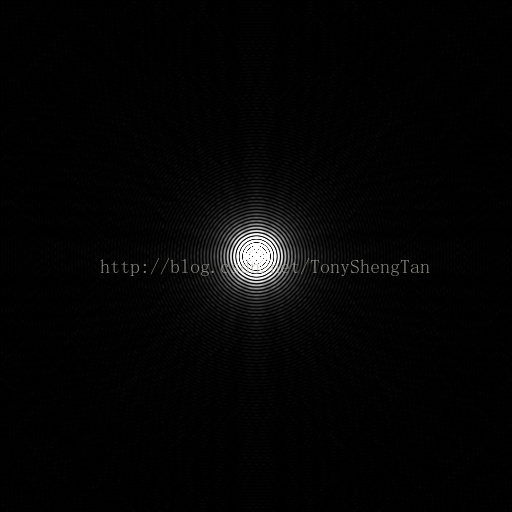


可以看出越宽(截止频率大)的滤波器频域振铃越步明显,相反,越窄的滤波器,空域振铃效果越大。
频域滤波进程
频率域滤波的进程:由于我们要得到的是图象,输入是图象,输出也是图象,这个进程叫图象处理,如果输出的时频谱或其他的,我们叫图象分析,滤波器的主要参数是类型和截止频率。
下面来看1下算法的完全计算进程:
原图:

空域填充:
用0对图片进行填充,得到4倍原图的新图象

频谱中心化
这是为了配合滤波器,由于滤波器1般被设计为中间为低频,4周为高频的模式
DFT:
过度到频域

设计滤波器
FIR滤波器,有限长单位冲激响应滤波器,又称为非递归型滤波器,图象处理中都使用这类滤波器产生1个高斯低通滤波器:

对位相乘:

IDFT:
将滤波结果重建为图象

空域取消填充:
将填充过的图象恢复

代码:
#include "filter.h"
static void showfilter(double *filter,int width,int height){
IplImage *show=cvCreateImage(cvSize(width, height),8,1);
for(int i=0;i<width;i++)
for(int j=0;j<height;j++){
cvSetReal2D(show, j, i, filter[i*width+j]*255.0);
}
cvNamedWindow("Filter", 1);
cvShowImage("Filter", show);
cvWaitKey(0);
cvSaveImage("/Users/Tony/DIPImage/step.jpg", show, 0);
cvReleaseImage(&show);
}
void MatrixMulti_R_C(double *src1,Complex *src2,Complex *dst,int size){//m(1,1)=a(1,1)*b(1,1);
for(int i=0;i<size;i++){
dst[i].real=src2[i].real*src1[i];
dst[i].imagin=src2[i].imagin*src1[i];
}
}
int ChangtoPower2(int size){
size--;//避免为2的幂的size会被扩大
int i=0;
while ((size/=2)>0) {
i++;
}
return 2<<i;
}
//将图象伸缩到2的幂次大小,并填充
void ResizeMatrix4FFT(IplImage *src,IplImage **dst){
int width=src->width;
int height=src->height;
int re_width=ChangtoPower2(width);
int re_height=ChangtoPower2(height);
IplImage *temp=cvCreateImage(cvSize(re_width, re_height), src->depth, src->nChannels);
cvResize(src, temp, 0);
*dst=cvCreateImage(cvSize(re_width*2, re_height*2), src->depth, src->nChannels);
cvZero(*dst);
for(int i=0;i<re_width;i++)
for(int j=0;j<re_height;j++)
cvSetReal2D(*dst, j, i, cvGetReal2D(temp, j, i));
cvReleaseImage(&temp);
}
//将扩充后的图象还原为左上角的
void CutImage421(IplImage *src,IplImage *dst){
//IplImage *temp=cvCreateImage(cvSize(src->width/2, src->height/2), src->depth, src->nChannels);
int width=dst->width;
int height=dst->height;
for(int i=0;i<width;i++)
for(int j=0;j<height;j++)
cvSetReal2D(dst, j, i, cvGetReal2D(src, j, i));
}
//频域滤波
void FrequencyFiltering(IplImage *src,IplImage *dst,int filter_type,double param1,int param2){
IplImage *temp=NULL;
//调剂至2的幂,并用黑色填充,避免周期缠绕
ResizeMatrix4FFT(src, &temp);
int fft_width=temp->width;
int fft_height=temp->height;
//产生滤波器
double *filter=(double *)malloc(sizeof(double)*fft_height*fft_width);
if(filter==NULL){
printf("frequency filter malloc faile");
exit(0);
}
//生成滤波器
switch(filter_type){
case ILPF:
IdealLPFilter(filter, fft_width, fft_height, param1);
break;
case BLPF:
if(param2<0)
param2=2;
ButterworthLPfilter(filter, fft_width, fft_height, param1, param2);
break;
case GLPF:
GaussianLPFilter(filter, fft_width, fft_height, param1);
break;
case IHPF:
IdealHPFilter(filter, fft_width, fft_height, param1);
break;
case BHPF:
if(param2<0)
param2=2;
ButterworthHPfilter(filter, fft_width, fft_height, param1, param2);
break;
case GHPF:
GaussianHPFilter(filter, fft_width, fft_height, param1);
break;
}
//FFT
Complex *temp_complex=(Complex*)malloc(sizeof(Complex)*fft_height*fft_width);//fft结果
if(temp_complex==NULL){
exit(0);
}
ImageFFT(temp, temp_complex);
//相乘
MatrixMulti_R_C(filter,temp_complex,temp_complex,fft_width*fft_height);
//IFFT
ImageIFFT(temp_complex, temp, temp->width, temp->height);
//还原图象
IplImage *result2=cvCreateImage(cvSize(temp->width/2, temp->height/2), temp->depth, temp->nChannels);
CutImage421(temp, result2);
cvResize(result2, dst, 0);
free(filter);
free(temp_complex);
cvReleaseImage(&temp);
cvReleaseImage(&result2);
}
空域滤波与频域滤波
空域和频域的桥梁是傅里叶变换,而纽带是卷积定理,对频域的特性,我们将其看作1个实验室,进行实验并产生小的滤波模板,将小的滤波模板对空域图象进行循环卷积,得到我们想要的结果,空域小模板多半是奇数大小的(3x3,5x5)的,其计算复杂度低,进程简单,用时较短,这就是之条件到的那个面试的问题的答案,如果我当时把这个进程给面试官讲清楚,估计我现在就是1名图象工作者了。
总结
这就是频域滤波的基础,后面的事情就是设计滤波器,满足不同的问题,有了基础,设计滤波器就要自己发挥了。
------分隔线----------------------------
------分隔线----------------------------