Manacher 算法模板
栏目:php教程时间:2017-02-23 09:17:27
简介
在字符串的题目中,有时会遇上 回文串 这样1个名词
顾名思义,回文串 就是 正读和反读都1样的字符串
而 最长回文子串 ,就是在1个字符串的所有子串中,是回文串且长度最长的那个
求最长回文子串最普通的方法是
O(N2) ,即枚举1个点往两边扩大但是在有些题目中,N 却10分的大
那末我们就要用到 时间空间复杂度都是
O(N) 的 Manecher 算法
用法
在处理回文串时,我们常常会被 中间字符是1个还是两个 这样的问题困扰
但是在机灵的 Manacher 算法 中,这个问题得到了完善的解决
在每两个字符中间插入1个不会出现的分隔符(如:#)
以后在头尾插入1个还是没有出现的分隔符(如:*)来避免 While 出界
这样处理起来就方便很多了!
设读入的字符串为
s[i] ,记录
p[i] 表示 以s[i] 为中心往两边扩大的最大长度视察可知,实际的回文串长度即为当前的
s[i]−1 再记录1个数
id ,p[id]+id 表示在i 位置前所有回文串中能延伸到的最右真个位置以下图:
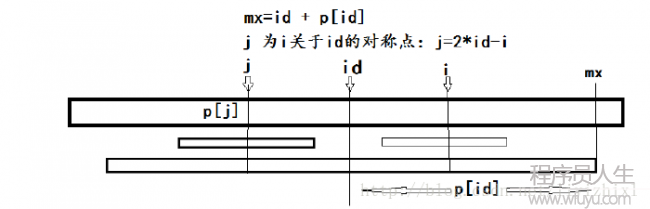
算法核心就是:
if(p[id]+id>i) p[i]=min(p[id∗2−i],p[id]+id−i); else p[i]=1; 当之前所有回文串中能延伸到的最右端覆盖过
i 时,则取最小值,否则p[i]=1 ,及自己本身这样不断保护
p[i] 和id ,就可以在O(N) 内求出 最长回文子串 了!至于为何时间是线性的,由于最有端
p[id]+id 最多只能移动 N 次,有效移动的操作就严格线性啦!!
下面附上模板:
void Manacher()
{
scanf("%s",s);
int len=strlen(s);
for(int i=len;i>=0;i--)
{
int k=i*2+1;
s[k+1]=s[i],s[k]='#';
}//插入分隔符
len*=2;
s[ans=id=0]='*';
for(int i=2;i<=len;i++)
{
if(p[id]+id>i) p[i]=min(p[id*2-i],p[id]+id-i); else p[i]=1;
while(s[i-p[i]]==s[i+p[i]]) p[i]++;
if(p[i]+i>p[id]+id) id=i;
if(p[i]>ans) ans=p[i];
}//处理、计算
}- 注释:
s[i],p[i],id 如题意义,ans 表示 最长回文子串 的长度,而len 是原串长度
总结
这个 Manacher 算法效力极高,时间空间都是
O(N) 线性的再者代码极短,所以使用起来10分方便,应多多使用!!!
------分隔线----------------------------
------分隔线----------------------------