数据结构学习笔记（一）：基本概念：什么是数据结构和算法，应用实例

栏目：php教程时间：2016-12-12 15:02:33

前言

由于要开始实习了，发现之前有些学过的东西。哪怕是我曾花了很大的力气学过的，由于长时间的没有被使用。致使很多知识都忘记了。所以准备在投简历面试前，把知识全部巩固1下。

在中国大学MOOC（慕课）网上，准备开始学习浙江大学的数据结构，由陈越、何钦铭老师主讲。（讲的非常好）

课程地址：
http://www.icourse163.org/learn/ZJU⑼3001?tid=1001757011#/learn/announce

基本概念

1.1 甚么是数据结构

数据结构并没有官方的定义。

1般来讲，我们通常描写“数据结构”的时候，总会带着“算法”1词，因而可知数据结构必定是跟算法相干的。

老师提了个小问题。

1.1.1 关于数据组织—例1：图书摆放

例1：如果我给你1些书，和1些存储这些书的空间，你要怎样存储这些书呢？

这里写图片描述

我选的是A（我当时1秒就觉得随意放啊。没斟酌那末多。。这其实也说明了，如果在处理问题之前，就没有1个比较完善的解决方案的话，那末真正遇到问题，就真的1脸懵逼了，大家不要学我TVT）

正确答案是。。

由于老师并没有告知我们书架的范围，而不1样范围的数据，数据组织的情势也不同。

难不是在于如何放书，而是在于放这个书如何使：插入（放新书）和查询书，这两个操作更方便

方法1：随意放（放简单了，查询累死），如果是小范围的书，2本，无所谓。大范围，就不行。

方法2：依照书名的拼音顺序排放（查找容易，插入难，由于要给书挪位）

方法3：把书架划分成几块区域，每块区域指定放某种种别的图书；在某种种别内，依照书名的拼音字母顺序排放

插入：先定种别，2分查找肯定位置，移出空位
查找书：先定种别，再2分查找

不过此时就有新的问题。如何划分种别（分多细好呢？分细很难找，分少了也不行）和每一个种别所占的位置（少了就又要挪位，多了又浪费）

这个小故事告知我们：解决问题方法的效力，跟数据组织的方式是直接相干的（这就是数据结构的意义所在）

关于空间使用—例2：PrintN函数的实现

例2：写程序实现1个函数PrintN，使得传入1个正整数为N的参数后，能顺序打印从1到N的全部正整数。

给两个代码

//代码1
void PrintN(int N)
{
int i;
    for(i=1;i<=N;i++)
    {
        printf("%d\n",i);
    }
    reutrn;
}

//代码2
void PrintN(int N)
{
    if(N)
    {
        printN(N-1);
        printf("%d\n",N);
    }
    return;
}

代码1和代码2初看之下，代码量差不多。

1是用循环实现的，2是用递归实现的。

而递归函数连临时变量都没有用（代码1中的临时变量i），令人容易理解，看起来简单明了。

那末两个代码。运行效力如何呢？

当N=10，100，1000，10000，100000（10万）时的区分

建议大家实验下，N=10和N=10万的时候

（N=10万的时候，递归函数罢工了，没有出正确结果）

结论：递归函数对电脑的空间占用是非常恐怖的，对善于写递归函数的人来讲，递归函数简单明了，对计算机来讲，它非常吃内存，效力低。

也说明了解决问题方法的效力，跟空间的利用效力有关（还记得例题1得到的结论么（温习1下）：解决问题方法的效力，跟数据组织的方式是直接相干的

1.1.3 关于算法效力—例3：计算多项式的值

例：写程序计算给定多项式在给定点x处的值

多项式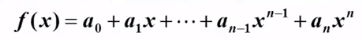：这里写图片描述

//代码1
double f(int n,double a[],double x)
{
    int i;
    double p=a[0];
    for(i=1;i<=n;i++)
        p+=(a[i]*pow(x,i));
    return p;
}

聪明的我们，应当先对多项式提取公因子进行处理

处理后的多项式：
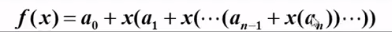
这里写图片描述

//代码2
double f(int n,double a[],double x)
{
    int i;
    double p=a[n];
    for(i=n;i>0;i--)
        p=a[i-1]+x*p;
    return p;
}

想要知道哪一个方法效力高。

C语言中提供了1个函数：

clock()：捕捉从程序开始运行到clock()被调用时所耗费的时间。这个时间单位是clock tick，即“时钟打点”。

常数CLK_TCK：机器时钟每秒所走的时钟打点数。

经常使用模板：

#include<stdio.h>
#include<time.h>

//clock_t是clock()函数返回的变量类型
clock_t start,stop;

//记录被测函数运行时间，以秒为单位
double duration;

int main()
{
    //不在测试范围的准备工作写在clock()调用之前
    start=clock();   //开始计时
    MyFunction();    //把被测函数加在这里
    stop=clock();    //停止计时
    duration=((double)(stop-start))/CLK_TCK;  //计算运行时间

    //其他不在测试范围的处理写在后面，例如输出duration的值
    return 0;
}

例3：写程序计算给定多项式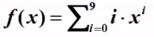这里写图片描述在给定点x=1.1处的值f(1.1)

//代码1

#include<math.h>  //由于使用了pow函数
double f(int n,double a[],double x)
{
    int i;
    double p=a[0];
    for(i=1;i<=n;i++)
        p+=(a[i]*pow(x,i));
    return p;
}

//代码2
double f(int n,double a[],double x)
{
    int i;
    double p=a[n];
    for(i=n;i>0;i--)
        p=a[i-1]+x*p;
    return p;
}

不过这两个函数由于运行时间都太快了。。不到1秒。。那末如何测呢？

重复

让被测函数重复运行屡次，使得测出的总的时钟打点间隔充分长，最后计算被测函数平均每次运行的时间便可

1.1.4 抽象数据类型—例4：“矩阵”的抽象数据类型定义

到底甚么是数据结构？

数据对象在计算机中的组织方式（像前面提的放书问题）
- 逻辑结构（如果1开始将书架想象成1条挨在1起的长架子，这样就是线性结构，1对1的；如果是将图书分类，那末1个类里面就会有很多书，这样是对多的，这样就是树型结构；如果我们需要统计，这本书被哪些人买过，买了这本书的人还买过哪些书，因而就是1本书对应很多人，那末1个人又对应很多书，所以这就是个很复杂的关系结构，叫做图结构）
- 物理存储结构（我们说的逻辑结构到底在计算机里如何存储）
数据对象一定与1系列加在其上的操作相干联
完成这些操作所用的方法就是算法

描写数据结构，我们通常使用抽象数据类型进行描写

抽象数据类型：

数据类型
- 数据对象集
- 数据集合相干联的操作集（这两个东西在C语言是分开处理的，但是在高级语言里，如JAVA，C++，以类的情势将它们封装在1起）
抽象：描写数据类型的方法不依赖于具体实现
- 与寄存数据的机器无关
- 与数据存储的物理结构无关
- 与实现操作的算法和编程语言均无关

只描写数据对象集合相干操作集“是甚么”，其实不触及“如何做到”的问题

例4：“矩阵”的抽象数据类型定义

这里写图片描述

1.2 甚么是算法

1.2.1 算法的定义—例1：选择排序算法的伪码描写

算法（Algorithm）

1个有限指令集
接受1些输入（有些情况下不需要输入）
产生输出
1定在有限步骤以后终止
每条指令必须
- 有充分明确的目标，不可以有歧义
- 计算性能处理的范围以内
- 描写应不依赖于任何1种计算机语言和具体的实现手段

例1：选择排序算法的伪码描写

//选择排序算法的伪码描写

void SelectionSort(int List[],int N)
{
    //将N个整数List[0]...List[N⑴]进行非递减排序
    for(i=0;i<N;i++)
    {
        //从List[i]到List[N⑴]中找最小元，并将其位置赋给MinPositon
        MinPositon=ScanForMin(List,i,N-1);
        //将未排序部份得最小元换到有序部份的最后位置
        Swap(List[i],List[MinPositon]);
    }
}

1.2.2 甚么是好的算法？

空间复杂度S(n)—-根据算法写成的程序在履行时占用存储单元的长度。这个长度常常与输入数据的范围有关。空间复杂度太高的算法可能致使使用的内存超限，造成程序非正常中断（前面的例2中的代码2使用的递归，传10万时）
时间复杂度T(n)—-根据算法写成的程序在履行时耗费时间的长度。这个长度常常也与输入数据的范围有关。时间复杂度太高的低效算法可能致使我们在有生之年都等不到运行结果（前面例3中代码1的时间复杂度为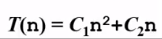，代码2的时间复杂度为）

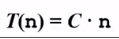在分析1般算法的效力时，我们常常关注下面两种复杂度
这里写图片描述

1.2.3 复杂度的渐进表示

复杂度的渐进表示法

这里写图片描述

经常使用复杂度函数

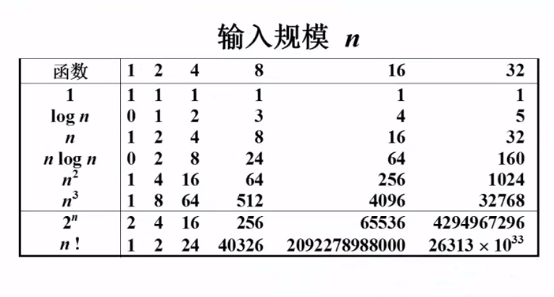
这里写图片描述

经常使用复杂度函数图表表示
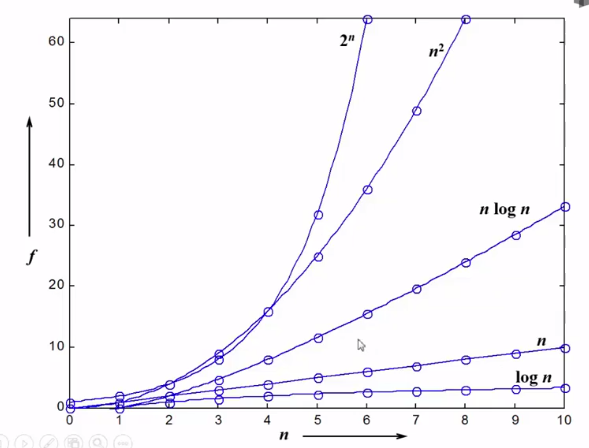
这里写图片描述

复杂度分析小诀窍

这里写图片描述

1.3 利用实例：最大子列和问题

1.3.1 利用实例—算法1&2

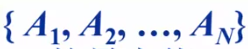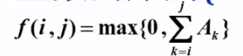问题：给定N个整数的序列这里写图片描述，求函数的最大值。
（不懂子列的意思的，可以想象成子集，比如说{A,B,C}，那末子列就有{A，}{B}，{C}，{A,B}，{A,C}，{B,C}，{A,B,C}，求最大子列和相当于最大自己包括的元素数。这个例题中最大的元素数为3）
算法1：

//算法1：暴力求出所有子列和，再找出最大的

int MaxSubseqSum1(int A[],int N)
{
    int ThisSum,MaxSum=0;
    int i,j,k;
    for(i=0;i<N;i++)       //i是子列左端位置
    {
        for(j=i;j<N;j++)   //j是子列右端位置
        {
            ThisSum=0;     //ThisSum是从A[i]到A[j]的子列和
            for(k=i;k<=j;k++)
                ThisSum+=A[k];
            if(ThisSum>MaxSum)  //如果刚得到的这个子列和更大，则更新结果
                MaxSum=ThisSum;

        }//j循环结束
    }    //i循环结束
    return MaxSum;
}

算法2：

//算法2
int MaxSubseqSum2(int A[],int N)
{
    int ThisSum,MaxSum=0;
    int i,j;
    for(i=0;i<N;i++)       //i是子列左端位置
    {
        ThisSum=0;         //ThisSum是从A[i]到A[j]的子列和
        for(j=i;j<N;j++)   //j是子列右端位置
        {
            ThisSum+=A[j]; //对不同的i,不同的j，只要在j⑴次循环的基础上累加1项便可
            if(ThisSum>MaxSum) //如果刚得到的子列和更大，则更新结果
                MaxSum=ThisSum;
        }//j循环结束
    }    //i循环结束
    return MaxSum;  
}

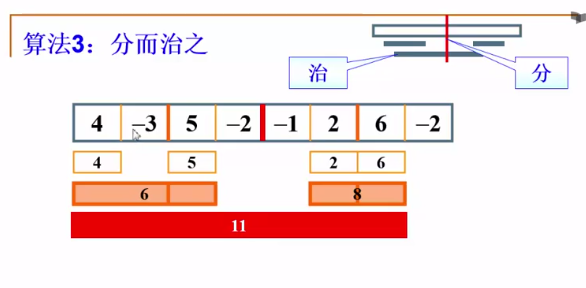
1.3.2 利用实例—算法3：分而治之

算法3：

分而治之可以将1个序列从中间分为2个，可能最大子序列就是这两个被分开当中最大的。也有可能正好逾越了两个。

这里写图片描述

int Max3( int A, int B, int C )
{ 
    /* 返回3个整数中的最大值 */
    return A > B ? A > C ? A : C : B > C ? B : C;
}

int DivideAndConquer( int List[], int left, int right )
{ 
    /* 分治法求List[left]到List[right]的最大子列和 */
    int MaxLeftSum, MaxRightSum; /* 寄存左右子问题的解 */
    int MaxLeftBorderSum, MaxRightBorderSum; /*寄存跨分界限的结果*/

    int LeftBorderSum, RightBorderSum;
    int center, i;

    if( left == right )  
    {  
        /* 递归的终止条件，子列只有1个数字 */
        if( List[left] > 0 )  
            return List[left];
        else 
            return 0;
    }

    /* 下面是"分"的进程 */
    center = ( left + right ) / 2; /* 找到中分点 */

    /* 递归求得两边子列的最大和 */
    MaxLeftSum = DivideAndConquer( List, left, center );
    MaxRightSum = DivideAndConquer( List, center+1, right );

    /* 下面求跨分界限的最大子列和 */
    MaxLeftBorderSum = 0;  
    LeftBorderSum = 0;
    for( i=center; i>=left; i-- ) 
    { 
        /* 从中线向左扫描 */
        LeftBorderSum += List[i];
        if( LeftBorderSum > MaxLeftBorderSum )
            MaxLeftBorderSum = LeftBorderSum;
    } /* 左侧扫描结束 */

    MaxRightBorderSum = 0; 
    RightBorderSum = 0;
    for( i=center+1; i<=right; i++ )
    { 
        /* 从中线向右扫描 */
        RightBorderSum += List[i];
        if( RightBorderSum > MaxRightBorderSum )
            MaxRightBorderSum = RightBorderSum;
    } /* 右侧扫描结束 */

    /* 下面返回"治"的结果 */
    return Max3( MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum );
}

int MaxSubseqSum3( int List[], int N )
{ 
    /* 保持与前2种算法相同的函数接口 */
    return DivideAndConquer( List, 0, N-1 );
}

1.3.3 利用实例—算法4：在线处理

算法4：在线处理

//算法4（在线处理）的伪码描写

int MaxSubseqSum4(int A[],int N)
{
    int ThisSum,MaxSum;
    int i;
    ThisSum=MaxSum=0;
    for(i=0;i<N;i++)
    {
        ThisSum+=A[i];       //向右累加
        if(ThisSum>MaxSum)
            MaxSum=ThisSum;  //发现更大的则更新当前结果
        else if(ThisSum<0)   //如果当前子列和为负
            ThisSum=0;       //则不可能使后面的部份和增大，抛弃之
    }
    return MaxSum;
}

------分隔线----------------------------

上一篇 【HDU 4283】You Are the One（区间DP）

下一篇 RxJava switchIfEmpty操作符实现Android检查本地缓存逻辑判断

------分隔线----------------------------