程序员人生网站导航

算法#115--最大流量问题（网络流算法）

栏目：php教程时间：2016-12-07 08:38:38

1.物理模型

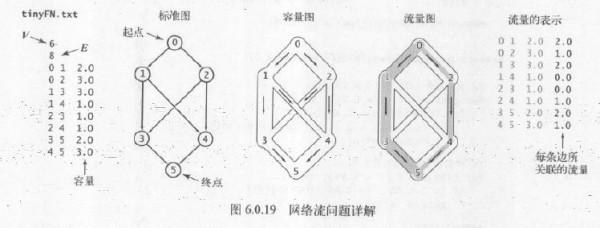
请想象1组相互连接大小不1的输油管道，每根管道有它自己的流量和容量，问从出发点到终点的最大流量是多少？以下流量图中，深色路径流量之和为最大路径。如何求得，下面内容将详细介绍。

2.数学模型

1个流量网络，是1张边的权重（这里称为容量）为正的加权有向图。1个st-流量网络有两个已知的顶点，即出发点s和终点t。

3.Ford-Fulkerson算法

也称为增广路径算法。它的定义是：网络中的初始流量为零，沿着任意从出发点到终点（且不含有饱和的正向边或是空逆向边）的增广路径增大流量，直到网络中不存在这样的路径为止。

也即，假定x为该路径上的所有边中未使用容量的最小值，那末只需将所有边的流量增大x，便可将网络中的总流量最少增大x。反复这个进程，直到所有出发点到终点的路径上最少有1条边是饱和的。

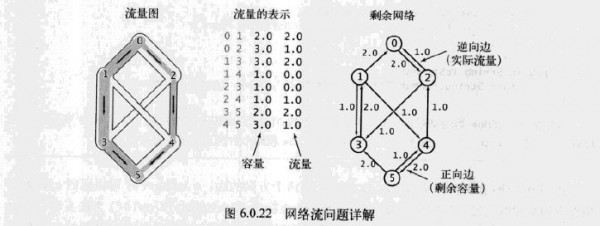
4.剩余网络

这里，与流量对应的边的方向和流量本身相反。代码以下FlowNetwork类。

5.代码实现

对Ford-Fulkerson算法最简单的实现可能就是最短增广路径算法了（最短指的是路径长度最小，而非流量或是容量）。增广路径的查找等价于剩余网络中的广度优先搜索（BFS）。


public class FordFulkerson 
{
    private boolean[] marked;   //在剩余网络中是不是存在从s到v的路径
    private FlowEdge[] edgeTo;  //从s到v的最短路径上的最后1条边
    private double value;       //当前最大流量

    public FordFulkerson(FlowNetwork G, int s, int t)
    {   //找出从s到t的流量网络G的最大流量配置
        while(hasAugmentingPath(G, s, t))
        {   //利用所有存在的增广路径
            //计算当前的瓶颈容量
            double bottle = Double.POSITIVE_INFINITY;
            for(int v = t; v != s; v = edgeTo[v].other(v))
            {
                bottle = Math.min(bottle, edgeTo[v].residualCapacityTo(v));
            }
            //增大流量
            for(int v = t; v != s; v = edgeTo[v].other(v))
            {
                edgeTo[v].addResidualFlowTo(v, bottle);
            }
            value += bottle;
        }       
    }

    private boolean hasAugmentingPath(FlowNetwork G, int s, int t)
    {
        marked = new boolean[G.V()];    //标记路径已知的顶点
        edgeTo = new FlowEdge[G.V()];   //路径上的最后1条边
        Queue<Integer> q = new Queue<Integer>();

        marked[s] = true;   //标记出发点
        q.enqueue(s);       //并将它入列
        while(!q.isEmpty())
        {
            int v = q.dequeue();
            for(FlowEdge e : G.adj(v))
            {
                int w = e.other(v);
                if(e.residualCapacityTo(w) > 0 && !marked[w])
                {//(在剩余网络中)对任意1条连接到1个未标记的顶点的边
                    edgeTo[w] = e;  //保持路径上的最后1条边
                    marked[w] = true;   //标记w，由于路径现在是已知的了
                    q.enqueue(w);   //将它入列
                }
            }
        }
        return marked[t];
    }

    public double value()
    {
        return value;
    }

    public boolean inCut(int v)
    {
        return marked[v];
    }

    public static void main(String[] args)
    {
        FlowNetwork G = new FlowNetwork(6);
        int[] from = new int[]{0, 0, 1, 1, 2, 2, 3, 4};
        int[] to = new int[]{1, 2, 3, 4, 3, 4, 5, 5};
        double[] capacity = new double[]{2.0, 3.0, 3.0, 1.0, 1.0, 1.0, 2.0, 3.0};
        for(int i = 0; i < from.length; i++)
        {
            FlowEdge edge = new FlowEdge(from[i], to[i], capacity[i]);
            G.addEdge(edge);
        }       

        int s = 0, t = G.V() - 1;
        FordFulkerson maxflow = new FordFulkerson(G, s, t);
        System.out.println("Max flow from " + s + " to " + t);
        for(int v = 0; v < G.V(); v++)
        {
            for(FlowEdge e : G.adj(v))
            {
                if(v == e.from() && e.flow() > 0)
                {
                    System.out.println(" " + e);
                }
            }
        }
        System.out.println("Max flow value = " + maxflow.value());
    }
}

输出：

Max flow from 0 to 5
 0->2 3.00 2.00
 0->1 2.00 2.00
 1->4 1.00 1.00
 1->3 3.00 1.00
 2->4 1.00 1.00
 2->3 1.00 1.00
 3->5 2.00 2.00
 4->5 3.00 2.00
Max flow value = 4.0

剩余网络类，其中的FlowEdge类的基础是加权边有向边。


public class FlowNetwork 
{
    private final int V;
    private int E;
    private Bag<FlowEdge>[] adj;

    @SuppressWarnings("unchecked")
    public FlowNetwork(int V)
    {
        this.V = V;
        this.E = 0;
        adj = (Bag<FlowEdge>[]) new Bag[V];
        for(int v = 0; v < V; v++)
        {
            adj[v] = new Bag<FlowEdge>();
        }
    }

    public int V()
    {
        return V;
    }

    public int E()
    {
        return E;
    }

    public void addEdge(FlowEdge e)
    {
        int v = e.either(), w = e.other(v);
        adj[v].add(e);
        adj[w].add(e);
        E++;
    }

    public Iterable<FlowEdge> adj(int v)
    {
        return adj[v];
    }

    public Iterable<FlowEdge> edges()
    {
        Bag<FlowEdge> b = new Bag<FlowEdge>();
        for(int v = 0; v < V; v++)
        {
            for(FlowEdge e : adj[v])
            {
                if(e.other(v) > v)
                {
                    b.add(e);
                }
            }
        }
        return b;
    }
}


public class FlowEdge 
{
    private final int v;
    private final int w;
    private final double capacity;
    private double flow;

    public FlowEdge(int v, int w, double capacity)
    {
        this.v = v;
        this.w = w;
        this.capacity = capacity;
        this.flow = 0;
    }

    public int from()
    {
        return v;
    }

    public int to()
    {
        return w;
    }

    public double capacity()
    {
        return capacity;
    }

    public double flow()
    {
        return flow;
    }

    public int either()
    {
        return v;
    }

    public int other(int vertex)
    {
        if(vertex == v)
        {
            return w;
        }
        else if(vertex == w)
        {
            return v;
        }
        else
        {
            throw new RuntimeException("Inconsistent edge");
        }
    }

    public double residualCapacityTo(int vertex)
    {
        if(vertex == v)
        {
            return flow;
        }
        else if(vertex == w)
        {
            return capacity - flow;
        }
        else
        {
            throw new RuntimeException("Inconsistent edge");
        }
    }

    public void addResidualFlowTo(int vertex, double delta)
    {
        if(vertex == v)
        {
            flow -= delta;
        }
        else if(vertex == w)
        {
            flow += delta;
        }
        else
        {
            throw new RuntimeException("Inconsistent edge");
        }
    }

    public String toString()
    {
        return String.format("%d->%d %.2f %.2f", v, w, capacity, flow);
    }
}

------分隔线----------------------------

上一篇 [置顶] C++基础复习心得4

下一篇 90%的企业都会考虑的数据平台建设方案

------分隔线----------------------------