Java与算法之(11) - 合并排序
栏目:php教程时间:2016-11-17 09:08:15
天下事,合久必分,分久必合。合并排序的基本思想正是先分再合。
例如对3, 1这个数列排序,首先是分,分为3和1两个数列,然后再合并并排序。合并需要额外的辅助空间,即建立1个两个数列长度之和的空数组用于存储合并结果。
合并分为3步:
1)两个数列在起始位置各分配1个"指针",对照指针位置的数字,取较小的数字存入辅助数组。数字被移出的1侧,指针右移1格,再次比较两个指针位置的数字,直到某1侧的指针移出数组之外结束。
2)把左边数组剩余的数字按顺序移动到辅助数组中
3)把右边数组剩余的数字按顺序移动到辅助数组中
进程以下图:
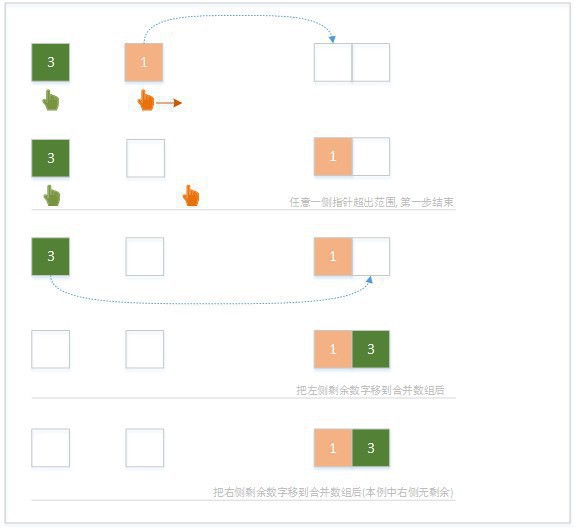
下面把两个数组的长度都增加到2,再看1下合并进程:

视察1下这个流程可以看出,这类合并排序的条件是左右两个数列本身是有序的。所以如果对4, 2, 3, 1排序,拆成4, 2和3, 1两个数列明显是不行的,需要继续拆分4, 2为4和2,然后合并为2, 4;拆分右边为3, 1,然后合并成1, 3。最后合并2, 4和1, 3。
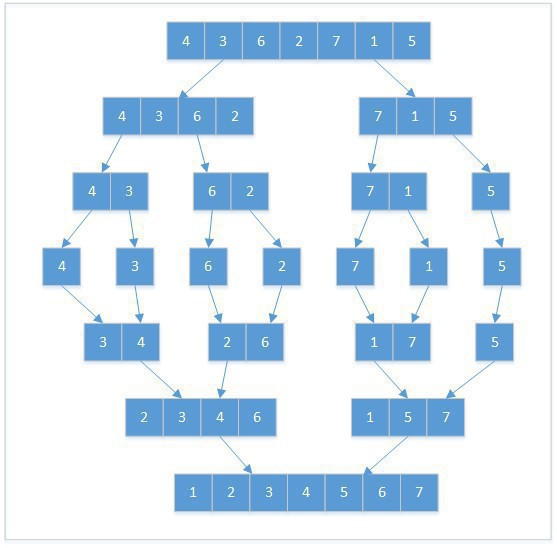
以4, 3, 6, 2, 7, 1, 5为例,完全的排序进程以下图:
来看代码:
import java.util.Arrays;
/**
* 合并排序法
* Created by autfish on 2016/9/20.
*/
public class MergeSort {
public static void main(String[] args) {
int[] numbers = new int[] {4, 3, 6, 2, 7, 1, 5};
System.out.println("排序前: " + Arrays.toString(numbers));
MergeSort ms = new MergeSort();
ms.sort(numbers, 0, numbers.length - 1);
System.out.println("排序后: " + Arrays.toString(numbers));
}
public void sort(int[] numbers, int from, int to) {
int middle = (from + to) / 2;
if (from < to) {
sort(numbers, from, middle);
sort(numbers, middle + 1, to);
//左边数列最大值小于右边数列最小值, 不需要通过合并来调剂顺序
if(numbers[middle] < numbers[middle + 1])
return;
merge(numbers, from, middle, to);
}
}
private void merge(int[] numbers, int from, int middle, int to) {
int[] temp = new int[to - from + 1];
int left = from;
int right = middle + 1;
int i = 0;
//从拆分到两边数列各剩1个数字开始合并; 当数列中有多个数字时, 1定是已排好序的
//从两边数列左边开始顺次取数对照, 挑选小的1个放入临时数组
while (left <= middle && right <= to) {
if (numbers[left] < numbers[right]) {
temp[i++] = numbers[left++];
} else {
temp[i++] = numbers[right++];
}
}
//把左侧数列剩余的数移入数组
while (left <= middle) {
temp[i++] = numbers[left++];
}
//把右侧数列剩余的数移入数组
while (right <= to) {
temp[i++] = numbers[right++];
}
System.arraycopy(temp, 0, numbers, from, temp.length);
}
}
运行:
排序前: [4, 3, 6, 2, 7, 1, 5]
排序后: [1, 2, 3, 4, 5, 6, 7]
合并排序平均情况和最坏情况的时间复杂度都是O(nlogn),由于需要额外的辅助空间,空间复杂度为O(n)。
------分隔线----------------------------
上一篇 收集的java问题和技巧
下一篇 NodeJs 畅谈异步
------分隔线----------------------------