Java与算法之(10) - 希尔排序
栏目:php教程时间:2016-11-03 08:44:24
希尔排序是插入排序的1种,是直接插入排序的改进版本。
对上节介绍的直接插入排序法,如果数据原来就已按要求的顺序排列,则在排序进程中不需要进行数据移动操作,便可得到有序数列。但是,如果最初的数据是按倒序排列的,则在进行插入排序时每次的比较都需要向后移动数据,这样,将致使算法的效力很低。
希尔排序的思想是把数列划分为若干个较小的数列,对每组数列使用直接插入排序算法排序,随着增量逐步减少,每组包括的数字愈来愈多,当增量减至1时,全部数列恰被分成1组,最后再使用1次直接插入排序对全部数列进行排序。
例如有4, 3, 6, 2, 7, 1, 5, 88个数字,第1次分成4组,即8/2组。以下图,相同色彩的数字为1组,下标为x的数字和下标为x+4的数字为1组。

对这4个数组分别做直接插入排序,即两两比较,如果大的在前则交换位置,得到:

然后缩小组数,4/2=2,缩小为两组。以下图:
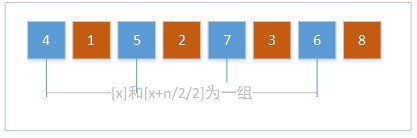
对这两个数组分别做直接插入排序,得到:
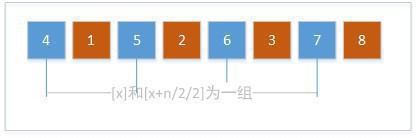
再次缩小组数,2/2=1,缩小为1组,那末所有数字都。以下图:

最后,对4, 1, 5, 2, 6, 3, 7, 8这个数列履行1次直接插入排序。
总结上面的规律,可以得出:
第1次分组数s = n / 2 == 0 ? n / 2 : n / 2 + 1
取数规则是[x]和[x+n/2]为1组
固然,这只是比较简单的分组方式,不1定是最优的。来看代码:
public class ShellSort {
private int[] numbers;
public ShellSort(int[] numbers) {
this.numbers = numbers;
}
/**
* 对数组分组并对每一个组做直接插入排序, 完成后缩小组的数量, 重复插入排序, 直到缩小到1个组
* 第1次分组数: section = n/2 == 0 ? n/2 : n/2+1, 分组规则: 每隔n/2挑1个数, 即[x]和[x+n/2]为1组
*/
public void sort() {
int section = this.numbers.length / 2;
int j;
int temp;
while(section >= 1) {
for(int i = section; i < this.numbers.length; i++) {
temp = this.numbers[i];
j = i - section;
while(j >= 0 && this.numbers[j] > temp) {
this.numbers[j + section] = this.numbers[j];
j = j - section;
}
this.numbers[j + section] = temp;
}
section /= 2;
}
System.out.print("排序后: ");
for(int x = 0; x < numbers.length; x++) {
System.out.print(numbers[x] + " ");
}
}
public static void main(String[] args) {
int[] numbers = new int[] { 4, 3, 6, 2, 7, 1, 5, 8 };
System.out.print("排序前: ");
for(int x = 0; x < numbers.length; x++) {
System.out.print(numbers[x] + " ");
}
System.out.println();
ShellSort ss = new ShellSort(numbers);
ss.sort();
}
}
运行:
排序前: 4 3 6 2 7 1 5 8
排序后: 1 2 3 4 5 6 7 8
希尔排序的时间复杂度,最坏是O(n^2),平均O(n^3/2)。
------分隔线----------------------------
------分隔线----------------------------