程序员人生网站导航

算法#14--详解各种字符串查找算法和代码实现

栏目：php教程时间：2016-10-06 09:13:49

1.算法汇总

首先，来看1张各种字符串查找算法的汇总。前面的文章已介绍过2叉树查找和红黑树查找。这里不在介绍。

本文重点介绍后面3种查找算法：线性探测法、R向单词查找树和3向单词查找树。

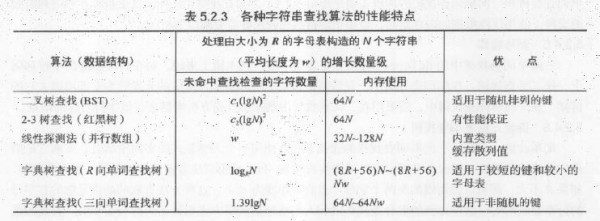
2.线性探测法

实现散列表的另外一种方式是用大小为M的数组保存N个键值对，其中M>N。依托数据中的空位解决碰撞冲突。基于这类策略的所有方法都统称为开放地址散列表。其中最简单的方法叫做线性探测法：当碰撞产生时，直接检查散列表的下1个位置（索引加1），可能产生3种结果：

命中，该位置的键和被查找的键相同；
未命中，键为空（该位置没有键）；
继续查找，该位置的键和被查找的键不同。

其核心思想是与其将内存用作链表，不如将它们作为散列表的空元素。即用散列函数找到索引，检查其中的键和被查找的键是不是相同。如果不同则继续查找（增加索引，到达数组结尾后再折回数组开头），直到找到该键或遇到1个空元素。进程以下图所示：

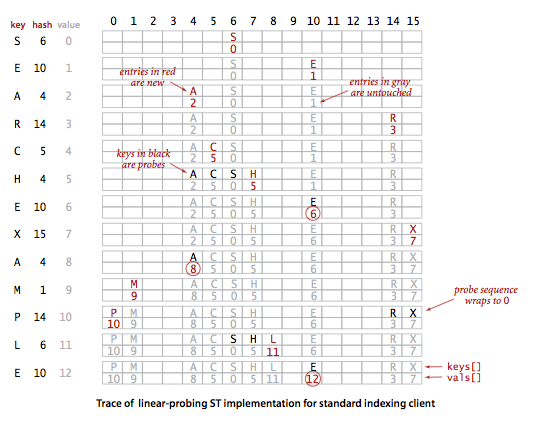
在基于线性探测法的散列表中履行删除操作比较复杂，如果将该键所在位置为为null是不行的。需要将簇中被删除键的右边的所有键重新插入散列表。

代码实现：


//基于线性探测的符号表
public class LinearProbingHashST<Key,Value> 
{
    private static final int INIT_CAPACITY = 16;

    private int n;// 键值对数量
    private int m;// 散列表的大小
    private Key[] keys;// 保存键的数组
    private Value[] vals;// 保存值的数组

    public LinearProbingHashST() 
    {
        this(INIT_CAPACITY);
    }

    @SuppressWarnings("unchecked")
    public LinearProbingHashST(int capacity) 
    {
        this.m = capacity;
        keys = (Key[]) new Object[capacity];
        vals = (Value[]) new Object[capacity];
    }

    public int hash(Key key)
    {
        return (key.hashCode() & 0x7fffffff) % m;
    }

    public void put(Key key, Value val)
    {
        if(key == null) 
        {
            throw new NullPointerException("key is null");
        }

        if(val == null)
        {
            delete(key);
            return;
        }

        // TODO扩容
        if(n >= m/2)
        {
            resize(2*m);
        }

        int i = hash(key);
        for (; keys[i] != null; i = (i + 1) % m) 
        {
            if(key.equals(keys[i]))
            {
                vals[i] = val;
                return;
            }
        }

        keys[i] = key;
        vals[i] = val;
        n++;
    }

    public void delete(Key key)
    {
        if(key == null) 
        {
            throw new NullPointerException("key is null");
        }

        if (!contains(key)) 
        {
            return;
        }

        // 找到删除的位置
        int i = hash(key);
        while (!key.equals(keys[i])) 
        {
            i = (i + 1) % m;
        }

        keys[i] = null;
        vals[i] = null;

        // 将删除位置后面的值重新散列
        i = (i + 1) % m;
        for (; keys[i] != null; i = (i + 1) % m) 
        {
            Key keyToRehash = keys[i];
            Value valToRehash = vals[i];
            keys[i] = null;
            vals[i] = null;
            n--;
            put(keyToRehash, valToRehash);
        }

        n--;
        // TODO缩容
        if(n>0 && n == m/8)
        {
            resize(m/2);
        }
    }

    public Value get(Key key)
    {
        if(key == null) 
        {
            throw new NullPointerException("key is null");
        }

        for (int i = hash(key); keys[i] != null; i = (i + 1) % m) 
        {
            if(key.equals(keys[i]))
            {
                return vals[i];
            }
        }
        return null;
    }

    public boolean contains(Key key)
    {
        if(key == null) 
        {
            throw new NullPointerException("key is null");
        }

        return get(key) != null;
    }   

    private void resize(int cap)
    {
        LinearProbingHashST<Key,Value> t;
        t = new LinearProbingHashST<Key,Value>(cap);
        for(int i = 0; i < m; i++)
        {
            if(keys[i] != null)
            {
                t.put(keys[i], vals[i]);
            }
        }
        keys = t.keys;
        vals = t.vals;
        m = t.m;
    }

     public static void main(String[] args) 
     { 
         LinearProbingHashST<String, String> st = new LinearProbingHashST<String, String>();
         String[] data = new String[]{"a", "b", "c", "d", "e", "f", "g", "h", "m"};
         String[] val = new String[]{"aaa", "bbb", "ccc", "ddd", "eee", "fff", "ggg", "hhh", "mmm"};
         for (int i = 0; i < data.length; i++)
         {            
            st.put(data[i], val[i]);
         } 

         for (int i = 0; i < data.length; i++)
         {
             System.out.println(data[i] + " " + st.get(data[i]));
         }     
     }
}

3.R向单词查找树

3.1 定义

与各种查找树1样，单词查找树也是由链接的结点所组成的数据结构。每一个结点只有1个父结点（根结点除外），每一个结点都含有R条链接，其中R为字母表的大小。每一个键所关联的值保存在该键的最后1个字母所对应的结点中。值为空的结点在符号表中没有对应的键，它们的存在是为了简化单词查找树中的查找操作。

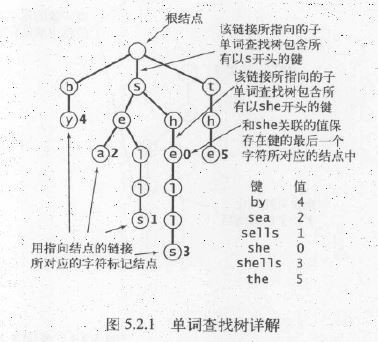
3.2 查找操作

单词查找树的查找操作非常简单，从首字母开始延着树结点查找就能够：

键的尾字符所对应的结点中的值非空，命中！
键的尾字符所对应的结点中的值为空，未命中！
查找结束于1条空链接，未命中！

3.3 插入操作

和2叉查找树1样，在插入之前要进行1次查找。

在到达键的尾字符之前就遇到了1个空链接。证明不存在匹配的结点，为键中还未被检查的每一个字符创建1个对应的结点，并将键对应的值保存到最后1个字符的结点中。
在遇到空链接之前就到达了键的尾字符。将该结点的值设为键对应的值（不管该值是不是为空）。

3.4 删除操作

删除的第1步是找到键所对应的结点并将它的值设为空null. 如果该结点含有1个非空的链接指向某个子结点，那末就不需要再进行其他操作了。如果它的所有链接均为空，那就需要从数据结构中删除这个结点。如果删除它使得它的父结点的所有链接也均为空，就要继续删除它的父结点，依此类推。

3.5 代码实现


//基于R向单词查找树的符号表
public class TrieST<Value> {
    private static int R = 256; //基数
    private Node root;
    private static class Node
    {
        private Object val;
        private Node[] next = new Node[R];
    }

    @SuppressWarnings("unchecked")
    public Value get(String key)
    {
        Node x = get(root, key, 0);
        if(x == null)
        {
            return null;
        }
        return (Value)x.val;
    }

    private Node get(Node x, String key, int d)
    {
        //返回以x作为根结点的字单词查找树中与key相干联的值
        if(x == null)
        {
            return null;
        }
        if(d == key.length())
        {
            return x;
        }
        char c = key.charAt(d);//找到第d个字符所对应的字单词查找树
        return get(x.next[c], key, d + 1);
    }

    public void put(String key, Value val)
    {
        root = put(root, key, val, 0);          
    }

    private Node put(Node x, String key, Value val, int d)
    {
        //如果key存在于以x为根结点的子单词查找树中则更新与它相干联的值
        if(x == null)
        {
            x = new Node();         
        }
        if(d == key.length())
        {
            x.val = val;
            return x;
        }
        char c = key.charAt(d);//找到第d个字符所对应的字单词查找树
        x.next[c] = put(x.next[c], key, val, d + 1);
        return x;
    }

    public void delete(String key)
    {  
        root = delete(root, key, 0); 
    }  

    private Node delete(Node x, String key, int d)
    {  
        if(x == null) 
        {
            return null;  
        }
        if(d == key.length())
        {
            x.val = null;  
        }
        else
        {  
            char c= key.charAt(d);  
            x.next[c] = delete(x.next[c], key, d+1);  
        }  
        if(x.val != null) 
        {
            return x;  
        }

        for(char c = 0; c < R; c++) 
        {
            if(x.next[c] != null) 
            {
                return x; 
            }
        }
        return null;  
    }  

    public static void main(String[] args) 
     {
        TrieST<Integer> newST = new TrieST<Integer>();
        String[] keys= {"Nicholas", "Nate", "Jenny", "Penny", "Cynthina", "Michael"};
        for(int i = 0; i < keys.length; i++)
        {
            newST.put(keys[i], i);
        }           
        newST.delete("Penny");
        for(int i = 0; i < keys.length; i++)
        {
            Object val = newST.get(keys[i]);
            System.out.println(keys[i] + " " + val);
        } 
     }

}

4.3向单词查找树

4.1 定义

3向单词查找树可以免R向单词查找树过度的空间消耗。它的每一个结点都含有1个字符、3条链接和1个值。3条链接分别对应当前字母小于、等于和大于结点字母的所有键。

4.1 查找、插入和删除操作

在查找时，首先比较键的首字母和根结点的字母。如果键的首字母较小，就选择左链接；如果较大，就选择右链接；如果相等则选择中链接。然后递归地使用相同的算法。如果遇到1个空链接或当键结束时结点的值为空，那末查找未命中。如果键结束时结点的值非空则查找命中。

插入1个新键时，首先进行查找，然后和单词查找树1样，在树中补全键末尾的所有结点。

在3向单词查找树中，需要使用在2叉查找树中删除结点的方法来删去与该字符对应的结点。

4.3 代码实现


//基于3向单词查找树的符号表
public class TST<Value> {
    private Node root;
    private class Node
    {
        char c;
        Node left, mid, right;
        Value val;
    }

    public Value get(String key)
    {
        Node x = get(root, key, 0);
        if(x == null)
        {
            return null;
        }
        return x.val;
    }

    private Node get(Node x, String key, int d)
    {
        if(x == null)
        {
            return null;
        }
        char c = key.charAt(d);
        if(c < x.c)
        {
            return get(x.left, key, d);
        }
        else if(c > x.c)
        {
            return get(x.right, key, d);
        }
        else if(d < key.length() - 1)
        {
            return get(x.mid, key, d + 1);
        }
        else
        {
            return x;
        }
    }

    public void put(String key, Value val)
    {
        root = put(root, key, val, 0);
    }

    private Node put(Node x, String key, Value val, int d)
    {
        char c = key.charAt(d);
        if(x == null)
        {
            x = new Node();
            x.c = c;
        }
        if(c < x.c)
        {
            x.left = put(x.left, key, val, d);
        }
        else if(c > x.c)
        {
            x.right = put(x.right, key, val, d);
        }
        else if(d < key.length() - 1)
        {
            x.mid = put(x.mid, key, val, d + 1);
        }
        else
        {
            x.val = val;
        }
        return x;
    }

     public static void main(String[] args) 
     {
            TST<Integer> newTST = new TST<Integer>();
            String[] keys= {"Nicholas", "Nate", "Jenny", "Penny", "Cynthina", "Michael"};
            for(int i = 0; i < keys.length; i++)
            {
                newTST.put(keys[i], i);
            }           

            for(int i = 0; i < keys.length; i++)
            {
                int val = newTST.get(keys[i]);
                System.out.println(keys[i] + " " + val);
            } 
     }
}

它的每一个结点只含有3个链接，因此所需空间远小于对应的单词查找树。使用3向单词查找树的最大好处是它能够很好地适应实际利用中可能出现的被查找键的不规则性。它可使用256个字符的ASCII编码或65536个字符的Unicode编码，而没必要担心分支带来的巨大开消。

------分隔线----------------------------

上一篇 【Bash百宝箱】shell内建命令之冒号

下一篇 背包9讲，总结

------分隔线----------------------------