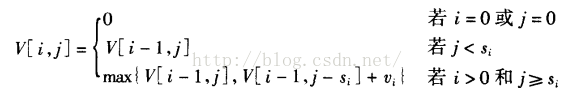01背包:
01背包是在M件物品取出若干件放在空间为W的背包里,每件物品的体积为W1,W2……Wn,与之相对应的价值为P1,P2……Pn。求能取得的最大总价值。
基本思路:
V[i,j]表示从前i件物品中取出的,能装入体积为j的背包的物品的最大总价值。
初始化条件:
V[i,0]和V[0,j]都为0,我们从其意义上就能够理解。
状态转移方程:
V[i,j]=max{ V[i⑴,j],V[i⑴,j-Wi]+Pi }
,前后分别为第i件物品不取和获得情况。
总的就是下面的递推式:
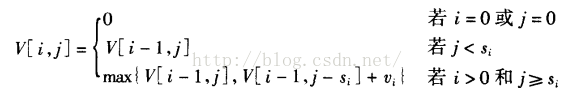
算法分析:
表的大小为n*C,所以算法的时间复杂度为Θ(nC),经过1些修改空间复杂度可以控制在Θ(C)内。
伪代码:

C++代码:
1.Θ(nC)的空间。
for(int i=0;i<=V;i++) dp[0][i]=0; // 初始条件
for(int i=1;i<=n;i++){
for(int v=0; v<=C[i]⑴; v++){
dp[i][v]=dp[i⑴][v];
}
for(int v=C[i];v<=V;v++){
dp[i][v]=max(dp[i⑴][v],dp[i⑴][v-C[i]]+W[i])
}
}
cout<<dp[n][V]<<endl;
2.在空间上做1些优化,Θ(C)的空间。
for(int i=0;i<=V;i++) dp[i]=0; // 初始条件
for(int i=1;i<=n;i++){
for(int v=V;v>=C[i];v--){
dp[v]=max(dp[v],dp[v-C[i]]+W[i])
}
}
cout<<dp[V]<<endl;
空间优化的基本思路:
我们知道原来代码中的2维数组的i是为了表示在前i个物品中做选择,同时也标志第i个物品是不是已选取了。
每次决策的时候是决定第i个物品是不是要选取。比如,对dp[i⑴][v-ci]我们知道第i个物品并没有选取,而对dp[i][v-ci]我们可以知道第i个物品已被选取了,我们每次自从前面1个状态(i⑴)来决策第i个是不是要选。
而空间优化的代码通过另外1套机制来保证1个物品只选1次。
我们可以看到第2个代码中的v是按逆序循环的,这样做是很有必要的:
这是由于要保证第i次循环中的状态dp[v]是由状态dp[v-c]递推而来。换句话说,这正是为了保证每件物品只选1次,保证在斟酌“选入第i件物品”这件策略时,根据的是1个没有已选入第i件物品的子结果dp[v-ci](如果已选入了,即dp[v]已完成状态转移方程,不会再进行)。
完全背包问题:
有N件物品和1个容量为V的背包。放入第i件物品所耗的容量为Ci,得到的价值为Wi,但是同1件物品可以放入任意多件,问您最多可以取得多少价值。
(1)2维数组的做法:时间复杂度O(NVlog2(V/C[i]))
基本思路
这里与01背包不同的是每件物品可以选任意多件,我们只需要在状态转移方程上进行1些改动:
V[i][j]=max{ V[i⑴][j-k*c[i]]+k*w[i] | 0<=k*c[i]<=v }
这里的k表示的是第i件物品选取的数量,在程序中,我们只需为k多进行1个循环,并注意k的取值范围,就能够解决完全背包问题。
伪代码:
F[0][] ← {0}
F[][0] ← {0}
for i←1 to N
do for j←1 to V
do for k←0 to j/C[i]
if(j >= k*C[i])
then F[i][k] ← max(F[i][k],F[i⑴][j-k*C[i]]+k*W[i])
return F[N][V]
(2)1维数组的做法:时间复杂度O(NV)
直接放代码:
C++代码:
for(int i=0;i<=V;i++) dp[i]=0; // 初始条件
for(int i=1;i<=n;i++){
for(int v=C[i];v<=V;v++){
dp[v]=max(dp[v],dp[v-C[i]]+W[i])
}
}
基本思路:
这里和01背包的空间优化代码差不多,改变的是v的循环顺序。前面v逆序循环的目的是为了保证每件物品只选择1次,改成正序循环后,每件物品选择的次数可以是任意的。
看下面这个例子dp[v-ci]后选择了第i件物品变成dp[v],而dp[(v+ci)-ci]依然可以选择第i件物品,变成dp[v+ci]。
多重背包:
有N件物品和1个容量为V的背包。放入第i件物品所耗的容量为Ci,得到的价值为Wi,但是第i件物品最多可以放入Mi件,问您最多可以取得多少价值。
基本思路:
(1)2维数组的做法
与前面两种背包的做法类似,只在状态转移方程上做1些更改。
dp[i][v]=max{ dp[i⑴][v-k*c[i]]+k*w[i] | 0<=k<=m[i] }
就不贴代码了。
(2)转化为01背包
空间优化的做法是将其转化为01背包,并采取2进制的做法进行拆分,即拆分成1件、2件、4件...。
for(int i=1;i<=n;i++){
int num=m[i]; // num为第i件物品由多少件
for(int k=1;num>=0;k*=2){
int mul=min(k,num) //k即为2进制数,之所以要和num取最小就类似与1000的时候512和489的情况,我们要选的时489.
for(int j=V;j>=C[i]*mul;j--){
dp[j]=max(dp[j],dp[j-C[i]*mul]+v[i]*mul)
}
num-=mul; // 分完那堆以后从总数上扣掉
}
}
最后贴1个代码:
#include <iostream>
using namespace std;
const int N = 3;//物品个数
const int V = 8;//背包容量
int Weight[N + 1] = {0,1,2,2};
int Value[N + 1] = {0,6,10,20};
int Num[N + 1] = {0,10,5,2};
int f[V + 1] = {0};
/*
f[v]:表示把前i件物品放入容量为v的背包中取得的最大收益。
f[v] = max(f[v],f[v - Weight[i]] + Value[i]);
v的为逆序
*/
void ZeroOnePack(int nWeight,int nValue)
{
for (int v = V;v >= nWeight;v--)
{
f[v] = max(f[v],f[v - nWeight] + nValue);
}
}
/*
f[v]:表示把前i件物品放入容量为v的背包中取得的最大收益。
f[v] = max(f[v],f[v - Weight[i]] + Value[i]);
v的为增序
*/
void CompletePack(int nWeight,int nValue)
{
for (int v = nWeight;v <= V;v++)
{
f[v] = max(f[v],f[v - nWeight] + nValue);
}
}
int MultiKnapsack()
{
int k = 1;
int nCount = 0;
for (int i = 1;i <= N;i++)
{
if (Weight[i] * Num[i] >= V)
{
//完全背包:该类物品原则上是无穷供应,
//此时满足条件Weight[i] * Num[i] >= V时,
//表示无穷量供应,直到背包放不下为止.
CompletePack(Weight[i],Value[i]);
}
else
{
k = 1;
nCount = Num[i];
while(k <= nCount)
{
ZeroOnePack(k * Weight[i],k * Value[i]);
nCount -= k;
k *= 2;
}
ZeroOnePack(nCount * Weight[i],nCount * Value[i]);
}
}
return f[V];
}
int main()
{
cout<<MultiKnapsack()<<endl;
system("pause");
return 1;
}
更进1步的了解,可以看看Tianyi Cui《背包问题9讲》。