017-Prim算法-贪心-《算法设计技巧与分析》M.H.A学习笔记
栏目:php教程时间:2016-06-30 08:42:24
基本思路:
定义结点集合U, V (U表示已选择加入MST的结点集合,V表示未选)
1. 任选1个结点加入U
2. 选择1条边权最小的边,他的两个结点分别属于U, V,并把属于V的那个结点加入U
3. 重复履行2直到V空
伪代码:
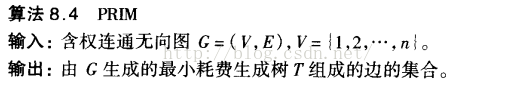

C++代码:
int g[mnx][mnx];
int n, m;
int d[mnx];
// 朴素 prim, 复杂度O(|V|^2) |V|:点数, |E|:边数
int prim() {
memset(d, 0x3f, sizeof d); //初始化
int ret = d[1] = 0; // 先把d[1]弄成0
for(int i = 1; i <= n; ++i) {
int u = ⑴;
for(int j = 1; j <= n; ++j) //找到d[u]最小的1个u
if((u == ⑴ || d[u] > d[j]) && d[j] != ⑴)
u = j;
ret += d[u];
d[u] = ⑴;
for(int j = 1; j <= n; ++j) // 更新和u邻接的节点的d[j]值
d[j] = min(d[j], g[u][j]);
}
return ret;
}
算法分析:
主要耗费在查找边权最小的边,这1步的2重循环耗费Θ(n2),所以算法的时间复杂度为Θ(n2)。
堆优化改进:
我们用小顶堆来完成查找最小边,和Dijkstra算法1样,算法共进行了n⑴次插入、n⑴次删除、m-n+1次Siftup运算。总的时间复杂度为O(mlogn)。
伪代码:


C++代码:
int fst[mnx], nxt[mxe], cost[mxe], to[mxe], e;
void init() {
memset(fst, ⑴, sizeof fst);
e = 0;
}
void add(int u, int v, int c) {
to[e] = v, nxt[e] = fst[u], cost[e] = c, fst[u] = e++;
}
struct node {
int u, dis;
node(int u, int dis):u(u), dis(dis) {}
bool operator < (const node &b) const {
return dis > b.dis;
}
};
//堆优化, 复杂度O(|E|log|V|), 稠密图时比较慢
int primHeap() {
memset(d, 0x3f, sizeof d);
d[1] = 0;
priority_queue<node> q;
q.push(node(1,0)); // 先选定第1个节点
int ret = 0;
while(!q.empty()) {
int u = q.top().u;
int dd = q.top().dis;
q.pop();
if(d[u] != dd) continue; // 如果是被更新之前的值的话就不取, continue掉
ret += dd;
d[u] = ⑴;
for(int j = fst[u]; ~j; j = nxt[j]) {
int v = to[j], c = cost[j]; // 更新
if(d[v] > c && d[v] != ⑴) {
d[v] = c;
q.push(node(v, c));
}
}
}
return ret;
}
------分隔线----------------------------
上一篇 php面试题与答案
------分隔线----------------------------