程序员人生网站导航

OpenGL学习脚印: 模型变换(model transformation)

栏目：php教程时间：2016-06-16 17:49:27

写在前面
前面为本节内容准备了向量和矩阵、线性变换等内容，本节开始学习OpenGL中的坐标处理。OpenGL中的坐标处理进程包括模型变换、视变换、投影变换、视口变换等内容，这个主题的内容有些多，因此分节学习，主题将分为5节内容来学习。本节主要学习模型变换。本节示例代码都可在我的github处下载。

通过本节可以了解到

模型变换的作用
模型变换的类型和计算方法

坐标处理的全局进程(了解，另文详述)

OpenGL中的坐标处理包括模型变换、视变换、投影变换、视口变换等内容，具体进程以下图1所示:

坐标变换
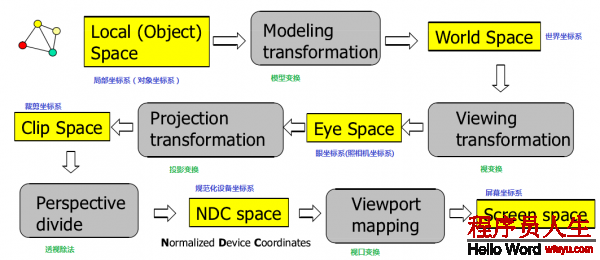
每个进程处理都有其缘由，这些内容计划将会在不同节里分别介绍，最后再整体掌控1遍。
今天我们学习第1个阶段——模型变换。

为何需要模型变换

我们在OpenGL中通过定义1组顶点来定义1个模型，或通过其他3D建模软件事前建好模型然后导入到OpenGL中。顶点属性定义了模型。如果我们要在1个场景中不同位置显示同1个模型怎样办？如果我们要以不同的比例、不同角度显示同1个模型又怎样办？
如果继续以类似的顶点属性数据定义同1个模型，调剂它满足上述需求的话，不但浪费显卡内存，而且这个调剂的工作量也很大，因此效力很低。更好地解决方法是，我们定义的模型根据需要可以履行放大、缩小等操作来不同比例显示，可以通过平移来放在不同位置，可以通过旋转来按不同角度显示。这类方式就是履行模型变换。
模型变换通过对模型履行平移(translation)、缩放(scale)、旋转(rotation)、镜像(reflection)、错切(shear)等操作，来调剂模型的进程。通过模型变换，我们可以依照公道方式指定场景中物体的位置等信息。

平移变换

平移就是将物体从1个位置 $p=(x,y,z)$ ，移动到另外一个位置 $p'=(x',y',z')$ 的进程，记为 $p'=p+d$ ，其中 $d=(x'-x, y'-y, z'-z)=(t_{x},t_{y},t_{z})$ 。使用齐次坐标系表示为:

p' = T p = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 100001000010 t x t y t z 1 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎡ ⎣ ⎢ ⎢ ⎢ x y z 1 ⎤ ⎦ ⎥ ⎥ ⎥ = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ x + t x y + t y z + t z 1 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥

$\begin{align} p' &= Tp \\ &= \begin{bmatrix} 1 & 0 & 0 & t_{x} \\ 0 & 1 & 0 & t_{y} \\ 0 & 0 & 1 & t_{z} \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} \\ &= \begin{bmatrix} x+t_{x} \\ y+t_{y} \\ z+t_{z} \\ 1 \end{bmatrix} \end{align}$

如果对向量和矩阵不熟习，可以回过去看前面介绍的向量和矩阵；如果对上面使用的齐次坐标系不熟习，可以回过去看前面介绍的线性变换部份。

本节的模型变换在OpenGL程序中，可使用GLM数学库实现。例如平移变换实现以下：

glm::mat4 model; // 构造单位矩阵
model = glm::translate(model, glm::vec3(-0.5f, 0.0f, 0.0f));

上述表示平移向量为(-0.5,0.0,0.0)，得到1个平移矩阵存储到model中。

在程序中我们绘制了4个矩形，通过平移将其放在不同位置，效果以下图所示：
模型变换

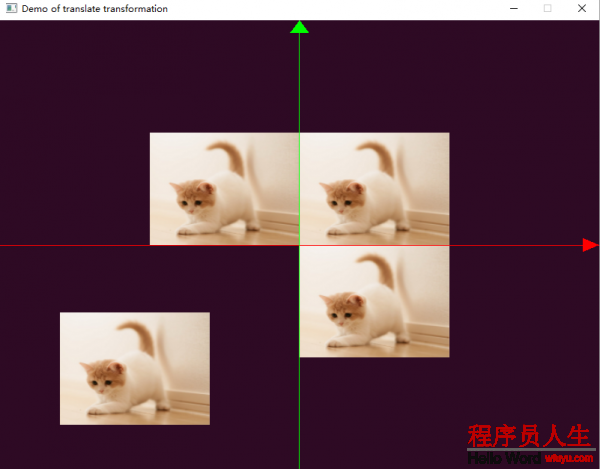
在上图示例中，我们使用不同的着色器还绘制了坐标轴，坐标轴通过箭头和轴线绘制。在xoy坐标系中，第1个象限为原图，第2个象限为平移(-0.5,0.0,0.0)后的矩形,第3象限为平移(-0.8,-0.8,0.0)后的矩形，第4个象限为平移(0.0,-0.5,0.0)后的矩形。

注意通过上面坐标处理的全局进程图1可以看到，实际顶点输出还需要经过视变换、投影变换进程等处理，本节主要讨论模型变换，因此我们在代码中，不斟酌视变换和投影变换，使用默许的视变换和投影变换，即这两个变换保持为单位矩阵。默许的方式就是我们1直在使用的正交投影方式。变换矩阵在着色器中使用uniform变量传递，在c++程序中使用glm::mat4与之对应。对uniform变量不熟习的话，可以回过头去看2D纹理部份的使用方法。

设置默许视变换和投影变换矩阵的代码以下：

   glm::mat4 projection;// 投影变换矩阵
   glm::mat4 view; // 视变换矩阵
   glm::mat4 model; // 模型变换矩阵
   glUniformMatrix4fv(
     glGetUniformLocation(shader.programId,"projection"),
     1, GL_FALSE, glm::value_ptr(projection));  
  glUniformMatrix4fv(
    glGetUniformLocation(shader.programId,"view"),
    1,GL_FALSE, glm::value_ptr(view));

绘制4个矩形的代码为：

   // 绘制第1个矩形
   glUniformMatrix4fv(
    glGetUniformLocation(shader.programId, "model"),
    1, GL_FALSE, glm::value_ptr(model));
  glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_SHORT, 0);

  // 绘制第2个矩形
 model = glm::mat4();
 model = glm::translate(model, glm::vec3(-0.5f, 0.0f, 0.0f));
glUniformMatrix4fv(
    glGetUniformLocation(shader.programId, "model"),
     1, GL_FALSE, glm::value_ptr(model));
glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_SHORT, 0);

// 绘制第3个矩形
model = glm::mat4();
model = glm::translate(model, glm::vec3(-0.8f, -0.8f, 0.0f));
glUniformMatrix4fv(
  glGetUniformLocation(shader.programId, "model"),   1, GL_FALSE, glm::value_ptr(model));
glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_SHORT, 0);

// 绘制第4个矩形
model = glm::mat4();
model = glm::translate(model, glm::vec3(0.0f, -0.5f, 0.0f));
glUniformMatrix4fv(
    glGetUniformLocation(shader.programId, "model"),1, GL_FALSE, glm::value_ptr(model));
glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_SHORT, 0);

这里绘制矩形使用的顶点属性数据，和纹理使用方法，可以回过头去查看上1节2D纹理映照内容。
本节绘制矩形的顶点着色器中都使用代码：

#version 330

layout(location = 0) in vec3 position;
layout(location = 1) in vec3 color;
layout(location = 2) in vec2 textCoord;

out vec3 VertColor;
out vec2 TextCoord;

uniform mat4 projection;
uniform mat4 view;
uniform mat4 model;

void main()
{
     gl_Position = 
     projection * view * model * vec4(position, 1.0);
     VertColor = color;
     TextCoord = textCoord;
}

本节绘制矩形的片元着色器中都使用代码：

#version 330

in vec3 VertColor;
in vec2 TextCoord;

uniform sampler2D tex;

out vec4 color;


void main()
{
  color = texture(tex, vec2(TextCoord.s, 1.0 -TextCoord.t) );
}

代码中使用坐标vec2(TextCoord.s, 1.0 -TextCoord.t)表示将纹理的y轴翻转，避免纹理倒立显示。
在座标和变换的数学基础1节中，我们已提到，对4x4仿射变换矩阵，可以表示平移(仿射变换)、缩放、旋转等线性变换，其中矩阵的情势为：

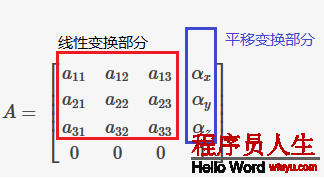
记住这1点，对矩阵情势理解会比较清楚。

缩放变换

缩放可以沿着3个坐标轴的方向独立进行，当缩放参数1致时是均匀缩放，否则是非均匀缩放。对以原点为中心的缩放来说，根据坐标和变换的数学基础，1节所得到的结论：线性变换矩阵为变换后基向量组成。缩放因子为 $(s_{x},s_{y},s_{z})$ ，则得到缩放后的+x轴基向量为 $(s_{x},0,0)$ ，+y轴基向量为 $(0,s_{y},0)$ ，+z轴缩放后基向量为(0

------分隔线----------------------------

上一篇 Redis

下一篇 享元模式(Flyweight)Java

------分隔线----------------------------