程序员人生网站导航

数据结构例程――从根节点到每个叶子节点的路径之逆

栏目：php教程时间：2016-02-27 15:46:21

本文是数据结构基础系列(6)：树和2叉树中第11课时2叉树遍历非递归算法和第12课时层次遍历算法的例程。

问题：设计算法输出从根节点到每一个叶子节点的路径之逆。
解法1：利用2叉树后序遍历非递归算法中，每个叶子节点出现时，栈中从栈顶到栈底，正好是叶子节点到根节点的逆序的性质编写。

［参考解答］（btreee.h见算法库）

#include <stdio.h>
#include "btree.h"

void AllPath1(BTNode *b)
{
    BTNode *St[MaxSize];
    BTNode *p;
    int flag,i,top=-1;  //栈指针置初值
    if (b!=NULL)
    {
        do
        {
            while (b!=NULL) //将*b的所有左节点进栈
            {
                top++;
                St[top]=b;
                b=b->lchild;
            }
            p=NULL;
            flag=1;
            while (top!=-1 && flag)
            {
                b=St[top];       //取出当前的栈顶元素
                if (b->rchild==p)
                {
                    if (b->lchild==NULL && b->rchild==NULL)
                    {
                        //若为叶子节点,输出栈中所有节点值
                        for (i=top; i>0; i--)
                            printf("%c->",St[i]->data);
                        printf("%c
",St[0]->data);
                    }
                    top--;
                    p=b;            //p指向刚访问过的节点
                }
                else
                {
                    b=b->rchild;          //b指向右孩子节点
                    flag=0;
                }
            }
        }
        while (top!=-1);
        printf("
");
    }
}

int main()
{
    BTNode *b;
    CreateBTNode(b,"A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))");
    printf("2叉树b: ");
    DispBTNode(b);
    printf("
");
    printf("从根节点到每一个叶子节点的路径之逆:
");
    AllPath1(b);
    DestroyBTNode(b);
    return 0;
}

解法2：利用2叉树层次遍历算法的思路解决。

采取非环形顺序队列qu
层次遍历2叉树
将所有已访问过的节点指针进队，并在队列中保存双亲节点的位置。
当找到1个叶子节点时，在队列中通过双亲节点的位置输出根节点到该叶子节点的路径之逆。

［参考解答］（btreee.h见算法库）

#include <stdio.h>
#include "btree.h"

void AllPath2(BTNode *b)
{
    struct snode
    {
        BTNode *node;   //寄存当前节点指针
        int parent;     //寄存双亲节点在队列中的位置
    } qu[MaxSize];      //定义非环形队列
    BTNode *q;
    int front,rear,p;   //定义队头和队尾指针
    front=rear=-1;      //置队列为空队列
    rear++;
    qu[rear].node=b;    //根节点指针进入队列
    qu[rear].parent=-1; //根节点没有双亲节点
    while (front!=rear) //队列不为空
    {
        front++;        //front是当前节点*q在qu中的位置
        q=qu[front].node;   //队头出队列,该节点指针仍在qu中
        if (q->lchild==NULL && q->rchild==NULL)
        {
            p=front;        //输出*q到根节点的路径序列
            while (qu[p].parent!=-1)
            {
                printf("%c->",qu[p].node->data);
                p=qu[p].parent;
            }
            printf("%c
",qu[p].node->data);
        }
        if (q->lchild!=NULL)    //*q节点有左孩子时将其进列
        {
            rear++;
            qu[rear].node=q->lchild;
            qu[rear].parent=front; //*q的双亲位置为front
        }
        if (q->rchild!=NULL)       //*q节点有右孩子时将其进列
        {
            rear++;
            qu[rear].node=q->rchild;
            qu[rear].parent=front; //*q的双亲位置为front
        }
    }
}

int main()
{
    BTNode *b;
    CreateBTNode(b,"A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))");
    printf("2叉树b: ");
    DispBTNode(b);
    printf("
");
    printf("从根节点到每一个叶子节点的路径之逆:
");
    AllPath2(b);
    DestroyBTNode(b);
    return 0;
}

注：在main函数中，创建的用于测试的2叉树以下――
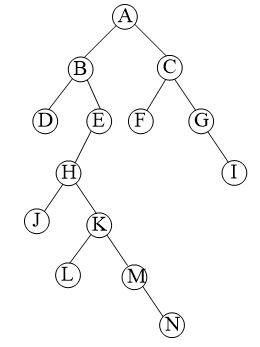
这里写图片描述

------分隔线----------------------------

上一篇 [置顶] 电商搜索之动态属性值（特征值）聚合

下一篇 程序员高效率工作工具推荐（必备工具）

------分隔线----------------------------