520E - Pluses everywhere/521C
- Pluses everywhere
Idea: Endagorion
Preparation: gchebanov, DPR-pavlin
Consider some way of placing all the pluses, and a single digit di (digits
in the string are numbered starting from 0 from left to right). This digit gives input of di・10l to
the total sum, where l is the distance to the nearest plus from the right, or to the end of string if there are no pluses there. If we sum up these quantities
for all digits and all ways of placing the pluses, we will obtain the answer.
For a given digit di and
some fixed l, how many ways are there to place the pluses? First of all, consider the case when the part containing the digit di is
not last, that is, i?+?l?<?n?-?1. There are n?-?1 gaps
to place pluses in total; the constraint about di and
the distance l means that after digits di, ..., di?+?l?-?1 there
are no pluses, while after the digit di?+?l there
should be a plus. That is, the string should look as follows:
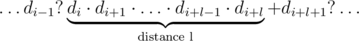
Here a dot means a gap without a plus, and a question mark means that it's not important whether there is a plus or not. So, out of n?-?1possible gaps
there are l?+?1 gaps which states are defined, and there is one plus used in these gaps. That means that the other (n?-?1)?-?(l?+?1)?=?n?-?l?-?2 gaps
may contain k?-?1 pluses in any possible way; that is, the number of such placements is 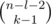 .
A similar reasoning implies that if the digit di is
in the last part, that is, i?+?l?=?n?-?1, the number of placements is
.
A similar reasoning implies that if the digit di is
in the last part, that is, i?+?l?=?n?-?1, the number of placements is  .
.
To sum up, the total answer is equal to
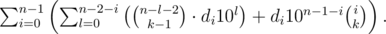
Let us transform the sum:

To compute these sums, we will need to know all powers of 10 up to n-th (modulo 109?+?7),
along with the binomial coefficients. To compute the binomials, recall that 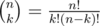 ,
so it is enough to know all the numbers k! for k upto n,
along with their modular inverses. Also we should use the prefix sums of di,
that is, the array
,
so it is enough to know all the numbers k! for k upto n,
along with their modular inverses. Also we should use the prefix sums of di,
that is, the array 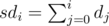 .
The rest is simple evaluation of the above sums.
.
The rest is simple evaluation of the above sums.
The total complexity is 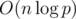 ,
because the common algorithms for modular inverses (that is, Ferma's little theorem exponentiation or solving a diophantine equation using the Euclid's algorithm) have theoritcal worst-case complexity of
,
because the common algorithms for modular inverses (that is, Ferma's little theorem exponentiation or solving a diophantine equation using the Euclid's algorithm) have theoritcal worst-case complexity of 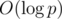 .
However, one can utilize a neat trick for finding modular inverses for first n consecutive numbers in linear time for a total complexity of O(n);
for the description of the method refer to this comment by Kaban⑸ (not
sure why it has a negative rating, I found this quite insightful; maybe anyone can give a proper source for this method?).
.
However, one can utilize a neat trick for finding modular inverses for first n consecutive numbers in linear time for a total complexity of O(n);
for the description of the method refer to this comment by Kaban⑸ (not
sure why it has a negative rating, I found this quite insightful; maybe anyone can give a proper source for this method?).
Challenge: now we want to find the sum of all expressions that are made by placing k pluses with a?≤?k?≤?b;
that is, we want to find the sum of the answers for the original problem with k?=?a,?...,?b; here a and b can
be any integers with 0?≤?a?≤?b?≤?n?-?1. There is an obviousO(n2) solution:
just find the answers for all k separately. Can you find a linear solution?
/* ***********************************************
Author :CKboss
Created Time :2015年03月04日 星期3 19时46分18秒
File Name :E.cpp
************************************************ */
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <string>
#include <cmath>
#include <cstdlib>
#include <vector>
#include <queue>
#include <set>
#include <map>
using namespace std;
typedef long long int LL;
const LL mod = 1e9+7LL;
const int maxn=100100;
int n,k;
LL a[maxn];
char str[maxn];
LL inv[maxn],presum[maxn];
LL jc[maxn],jcv[maxn],e[maxn];
void init()
{
/// inv jc e
inv[1]=1; jc[0]=1; jcv[0]=1;
jc[1]=1; jcv[1]=1; e[0]=1; e[1]=10;
for(int i=2;i<maxn;i++)
{
inv[i]=inv[mod%i]*(mod-mod/i)%mod;
jc[i]=(jc[i⑴]*i)%mod;
jcv[i]=(jcv[i⑴]*inv[i])%mod;
e[i]=(e[i⑴]*10LL)%mod;
}
}
LL COMB(LL n,LL m)
{
if(m<0||m>n) return 0LL;
if(m==0||m==n) return 1LL;
/// n!/((n-m)!*m!)
LL ret=((jc[n]*jcv[n-m])%mod*jcv[m])%mod;
return ret;
}
void solve(int n,int k)
{
LL ans=0;
if(k==0)
{
for(int i=n⑴;i>=0;i--)
ans=(ans+(e[n⑴-i]*a[i])%mod)%mod;
cout<<ans%mod<<endl;
return ;
}
for(int l=0;l<=n⑵;l++)
ans=(ans+(e[l]*COMB(n-l⑵,k⑴)%mod*presum[n-l⑵])%mod)%mod;
for(int i=0;i<=n⑴;i++)
ans=(ans+((a[i]*e[n⑴-i])%mod*COMB(i,k))%mod)%mod;
cout<<ans%mod<<endl;
}
int main()
{
//freopen("in.txt","r",stdin);
//freopen("out.txt","w",stdout);
init();
scanf("%d%d",&n,&k);
scanf("%s",str);
for(int i=0;i<n;i++)
{
a[i]=str[i]-'0';
if(i==0) presum[i]=a[i];
else presum[i]=(presum[i⑴]+a[i])%mod;
}
solve(n,k);
return 0;
}
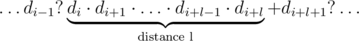
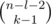 .
A similar reasoning implies that if the digit
.
A similar reasoning implies that if the digit  .
.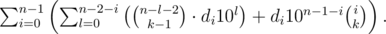

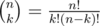 ,
so it is enough to know all the numbers
,
so it is enough to know all the numbers 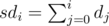 .
The rest is simple evaluation of the above sums.
.
The rest is simple evaluation of the above sums.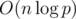 ,
because the common algorithms for modular inverses (that is, Ferma's little theorem exponentiation or solving a diophantine equation using the Euclid's algorithm) have theoritcal worst-case complexity of
,
because the common algorithms for modular inverses (that is, Ferma's little theorem exponentiation or solving a diophantine equation using the Euclid's algorithm) have theoritcal worst-case complexity of 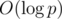 .
However, one can utilize a neat trick for finding modular inverses for first
.
However, one can utilize a neat trick for finding modular inverses for first