【日常学习】【条件最短路dij】POJ1062 昂贵的聘礼(2002年浙江省队选拔赛) 题解
耗时3节课 充分体现出粗心酿成大错这个道理 1开始1直不知道为何数组越界 原来是minn和ninj写反了 后来又由于读入函数出问题 反复调试 今后1定要注意
题目还是放上吧:
年轻的探险家来到了1个印第安部落里。在那里他和酋长的女儿相爱了,因而便向酋长去求亲。酋长要他用10000个金币作为聘礼才答应把女儿嫁给他。探险家拿不出这么多金币,便要求酋长下降要求。酋长说:“嗯,如果你能够替我弄到大祭司的皮袄,我可以只要8000金币。如果你能够弄来他的水晶球,那末只要5000金币就好了。”探险家就跑到大祭司那里,向他要求皮袄或水晶球,大祭司要他用金币来换,或替他弄来其他的东西,他可以下降价格。探险家因而又跑到其他地方,其他人也提出了类似的要求,或直接用金币换,或找到其他东西就能够下降价格。不过探险家没必要用多样东西去换1样东西,由于不会得到更低的价格。探险家现在很需要你的帮忙,让他用最少的金币娶到自己的心上人。另外他要告知你的是,在这个部落里,等级观念10分森严。地位差距超过1定限制的两个人之间不会进行任何情势的直接接触,包括交易。他是1个外来人,所以可以不受这些限制。但是如果他和某个地位较低的人进行了交易,地位较高的的人不会再和他交易,他们认为这样等因而间接接触,反过来也1样。因此你需要在斟酌所有的情况以后给他提供1个最好的方案。
为了方便起见,我们把所有的物品从1开始进行编号,酋长的承诺也看做1个物品,并且编号总是1。每一个物品都有对应的价格P,主人的地位等级L,和1系列的替换品Ti和该替换品所对应的“优惠”Vi。如果两人地位等级差距超过了M,就不能“间接交易”。你必须根据这些数据来计算出探险家最少需要多少金币才能娶到酋长的女儿。
输入包括了多个测试数据。每一个测试数据的第1行是两个整数M,N(1<=N<=100),顺次表示地位等级差距限制和物品的总数。接下来依照编号从小到大顺次给出了N个物品的描写。每一个物品的描写开头是3个非负整数P、L、X(X<N),顺次表示该物品的价格、主人的地位等级和替换品总数。接下来X行每行包括两个整数T和V,分别表示替换品的编号和“优惠价格”。
对每一个测试数据,在单唯一行内输出最少需要的金币数。
1 4
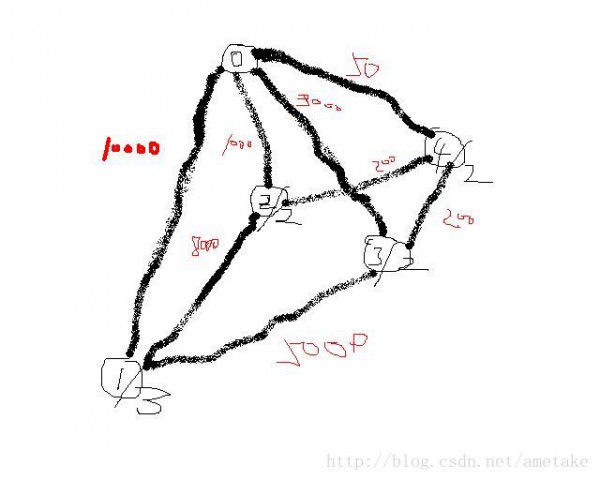
10000 3 2 //酋长的承诺
2 8000
3 5000
1000 2 1 //大祭司的皮袄
4 200
3000 2 1 //大祭司的水晶球
4 200
50 2 0 // 其他某件物品
5250
方便大家理解,画了1张很低劣的图,大家凑活看1下
代码放上:
在这里还要特别说明1下大整数常量的定义
const
int
maxn=0x3f3f3f3f;
这真是极好的存在= =援用1下1篇已消失的博文的解释(顺便吐槽域名重定向去了甚么鬼地方):
0x3f3f3f3f的10进制是1061109567,也就是10^9级别的(和0x7fffffff1个数量级),而1般场合下的数据都是小于10^9的,所以它可以作为无穷大使用而不致出现数据大于无穷大的情形。
另外一方面,由于1般的数据都不会大于10^9,所以当我们把无穷大加上1个数据时,它其实不会溢出(这就满足了“无穷大加1个有穷的数仍然是无穷大”),事实上0x3f3f3f3f+0x3f3f3f3f=2122219134,这非常大但却没有超过32-bit int的表示范围,所以0x3f3f3f3f还满足了我们“无穷大加无穷大还是无穷大”的需求。
最后,0x3f3f3f3f还能给我们带来1个意想不到的额外好处:如果我们想要将某个数组清零,我们通常会使用memset(a,0,sizeof(a))这样的代码来实现(方便而高效),但是当我们想将某个数组全部赋值为无穷大时(例如解决图论问题时邻接矩阵的初始化),就不能使用memset函数而得自己写循环了(写这些不重要的代码真的很痛苦),我们知道这是由于memset是按字节操作的,它能够对数组清零是由于0的每一个字节都是0,现在好了,如果我们将无穷大设为0x3f3f3f3f,那末奇迹就产生了,0x3f3f3f3f的每一个字节都是0x3f!所以要把1段内存全部置为无穷大,我们只需要memset(a,0x3f,sizeof(a))。
所以在通常的场合下,0x3f3f3f3f真的是1个非常棒的选择。
总结起来就是3句话
1 够大,1般这么大你不会用到
2 够大但不容易溢出
3 方便数组赋值(如果你用FF会变成负数,符号位也会成1)
1轮开始了,该来的总会来的。
欢迎小花加入C党大家族,本科同学你现在是1个人了,摸头・・・祝小花的喜家家之路1帆风顺。
――君子博学而日参省乎己,则知明而行无过矣。
上一篇 计算机指令仿真