欧拉函数

先来介绍几个与欧拉函数有关的定理：

定理1：设m与n是互素的正整数，那末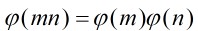

定理2：当n为奇数时，有。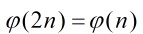

由于2n是偶数，偶数与偶数1定不互素，所以只斟酌2n与小于它的奇数互素的情况，则恰好就等于n的欧拉函数值。

定理3：设p是素数，a是1个正整数，那末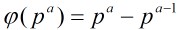

关于这个定理的证明用到容斥：

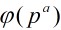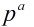由于表示小于与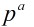互素数的正整数个数，所以用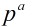减去与它不互素的数的个数就好了。

那末小于与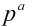不互素数的个数就是p的倍数个数，有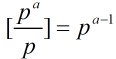个。所以定理得证。

定理4：设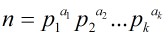为正整数n的素数幂分解，那末

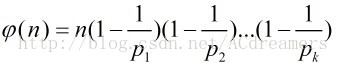
这个定理可以根据定理1和定理3证明，其实用到的就是容斥。如果对容斥熟习，其实完全就能够直接容斥。

定理5：设n是1个正整数，那末

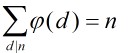
这个其实可以看莫比乌斯反演就明白了。

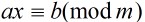定理6：设m是正整数，(a,m)=1，则：是同于方程的解。

定理7：如果n大于2，那末n的欧拉函数值是偶数。

求欧拉函数值：

利用递推法求欧拉函数值：

算法原理：开始令i的欧拉函数值等于它本身，如果i为偶数，可以利用定理2变成求奇数的。

若p是1个正整数满足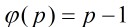，那末p是素数，在遍历进程中如果遇到欧拉函数值等于本身的情况，那末

说明该数为素数。把这个数的欧拉函数值改变，同时也把能被该素因子整除的数改变。