剑指offer 面试题21.22―栈操作以及判断弹出序列
栏目:php教程时间:2015-06-18 08:51:15
题目:
1.定义栈数据结构,请在该类型中实现1个能够得到栈的最小元素的min函数。在该栈中,调用min、push和pop的时间复杂度都是O(1)。
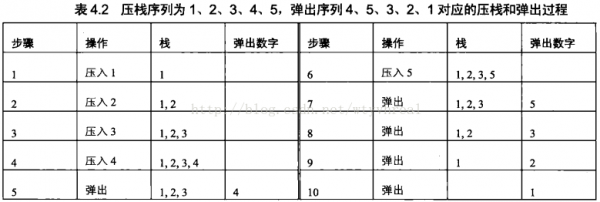
2.输入两个整数序列,第1个序列表示栈的压入顺序,请判断第2个序列是不是为该栈的弹出顺序。假定压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,
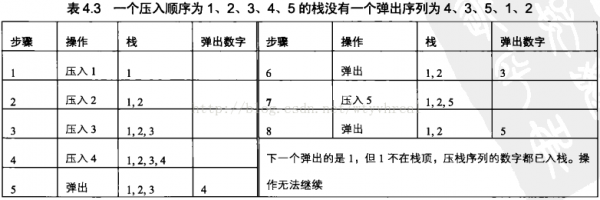
序列 4,5,3,2,1是该压栈序列对应的1个弹出序列,但4,3,5,1,2就不多是该压栈序列的弹出序列。
题目1解答:

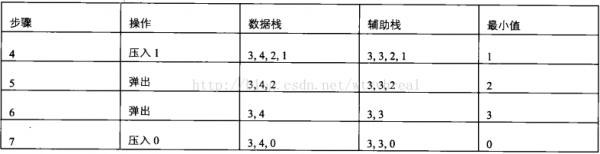
//m_data数据栈,m_min辅助栈
push(int value)
{
m_data.push(value);
if(m_min.size()==0 || value<m_min.top())
m_min.push(value);
else
m_min.push(m_min.top());
}
pop()
{
m_data.pop();
m_min.top();
}
min()
{
return m_min.top();
}
题目2解答:
我们可以建立1个辅助栈来存储入栈的部份序列,可以o(n)的时间复杂度内解决问题。出栈序列的元素首先与辅助栈(若不空)的栈顶元素比较,若不等再与入栈序列的元素比较。若与入栈序列的元素仍不相等,则当前入栈序列的元素进入辅助栈,出栈序列确当前元素与入栈序列的后面元素继续比较。若辅助栈的栈顶元素和入栈序列的全部元素都不与出栈序列确当前元素相等,则该序列不是1个正确的出栈序列;若所有出栈序列元素都比较完,则是1个正确的出栈序列。
#include <iostream>
#include <algorithm>
#include <string>
#include <stack>
using namespace std;
int a[100010],b[100010];
stack<int> s;
int main()
{
int n,i,j;
while(cin>>n)
{
for( i=0; i<n; i++ )
cin>>a[i];
for( i=0; i<n; i++ )
cin>>b[i];
i=j=0;
while( !s.empty() ) //这个很关键,由于有多个测试用例,所以需要清空上个测试用例的栈。
s.pop();
while(i<=n)
{
if( !s.empty() && b[j]==s.top() )
{
s.pop();
j++;
}
else
{
if( i==n )
break;
s.push(a[i]);
i++;
}
}
if( j == n )
cout<<"Yes"<<endl;
else
cout<<"No"<<endl;
}
return 0;
}

------分隔线----------------------------
------分隔线----------------------------