剑指offer 面试题29―数组中出现次数超过一半的数字
栏目:php教程时间:2015-06-08 08:35:13
题目:
数组中有1个数字出现的次数超过数组长度的1半,请找出这个数字。例如输入1个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次,超过数组长度的1半,因此输出2。
解法1:
解法2:O(n)
基本思想:
消除原理:在遍历数组的时候保存两个值:1个是数组中的1个数字,1个是次数。当我们遍历到下1个数字的时候,如果下1个数字和我们之前保存的数字相同,则次数加1。如果下1个数字和我们之前保存的数字不同,则次数减1。如果次数为零,我们需要保存下1个数字,并把次数设为1。由于我们要找的数字出现的次数比其他所有数字出现的次数之和还要多,那末要找的数字肯定是最后1次把次数设为1时对应的数字。
固然最后要再遍历1遍验证这个数的出现次数是不是大于数组的1半。
#include <iostream>
using namespace std;
bool CheckMoreThanHalf(int a[],int len,int key)
{
int times=0;
for(int i=0;i<len;i++)
{
if(a[i]==key)
times++;
}
bool flag=true;
if(times*2<=len)
flag=false;
return flag;
}
int foo(int a[],int len)
{
if(len<=0)
return ⑴;
int result=a[0];
int times=2;
for(int i=1;i<len;i++)
{
if(times==0)
{
result=a[i];
times=1;
}
else if(a[i]==result)
times++;
else
times--;
}
if(!CheckMoreThanHalf(a,len,result))
result=0;
return result;
}
int main()
{
int a[]={1,2,3,2,2,2,5,4,2};
int b[]={1,2,3,4};
int lenA = sizeof(a)/sizeof(a[0]);
int lenB = sizeof(b)/sizeof(b[0]);
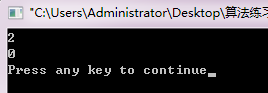
cout<<foo(a,lenA)<<endl;
cout<<foo(b,lenB)<<endl;
return 0;
}
解法3:基于partition函数,O(n)
基本思想:
如果1个数字才数组中出现的次数超过了数组长度的1半,那末对这个数组进行排序,位于数组中间位置的那个数就是出现次数超过1半的那个数。对数组排序的时间复杂度是O(nlog(n)),但是对这道题目,还有更好的算法,能够在时间复杂度O(n)内求出。我们写过快速排序算法,其中的Partition()方法是1个最重要的方法,该方法返回1个index,能够保证index位置的数是已排序完成的,在index左侧的数都比index所在的数小,在index右侧的数都比index所在的数大。那末本题就能够利用这样的思路来解。
- 通过Partition()返回index,如果index==mid,那末就表明找到了数组的中位数;如果index<mid,表明中位数在[index+1,end]之间;如果index>mid,表明中位数在[start,index⑴]之间。知道最后求得index==mid循环结束。
- 根据求得的index,遍历1遍数组,每当出现1个等于index所指向的数时time++,最后判断time是不是大于数组长度的1半,如果大于则表明index所指向的数就是所求的数,如果不是,则表明不存在1个数出现的次数超过数组长度的1半。
#include <iostream>
using namespace std;
bool CheckMoreThanHalf(int a[],int len,int key)
{
int times=0;
for(int i=0;i<len;i++)
{
if(a[i]==key)
times++;
}
bool flag=true;
if(times*2<=len)
flag=false;
return flag;
}
/*
int par(int a[],int len,int low,int high)
{
int t=a[low];
while(low<high)
{
while(low<high&&a[high]>=t)
high--;
a[low]=a[high];
while(low<high&&a[low]<=t)
low++;
a[high]=a[low];
}
a[low]=t;
return low;
}*/
int par(int a[],int len,int low,int high)
{
int t=a[low];
int i=low,j=high;
while(i!=j)
{
while(i<j&&a[j]>=t) j--;
while(i<j&&a[i]<=t) i++;
if(i<j)
{
int temp=a[i];
a[i]=a[j];
a[j]=temp;
}
}
a[low]=a[i];
a[i]=t;
return i;
}
int foo(int a[],int len)
{
if(len<=0)
return ⑴;
int mid = len>>1;
int start=0;
int end=len⑴;
int index=par(a,len,start,end);
while(index!=mid)
{
if(index>mid)
{
end=index⑴;
index=par(a,len,start,end);
}
else
{
start=index+1;
index=par(a,len,start,end);
}
}
int result=a[mid];
if(!CheckMoreThanHalf(a,len,result))
result=0;
return result;
}
int main()
{
int a[]={1,2,3,2,2,2,5,4,2};
int b[]={1,2,3,4};
int lenA = sizeof(a)/sizeof(a[0]);
int lenB = sizeof(b)/sizeof(b[0]);
cout<<foo(a,lenA)<<endl;
cout<<foo(b,lenB)<<endl;
return 0;
}
------分隔线----------------------------
------分隔线----------------------------