【C#】 25. 根据Option组成的投资组合的payoff,识别组成成分
栏目:php教程时间:2015-06-01 08:29:27
今天终究做了1个很久之前就想完成的option利用!
假定现在有1个全部由Option构成的投资组合,这些option的underlying都是同1个股票,有相同的maturity。
在Excel中写个函数,它可以根据portfolio在不同underlying price时的Payoff来辨认投资组合中各个option组成。
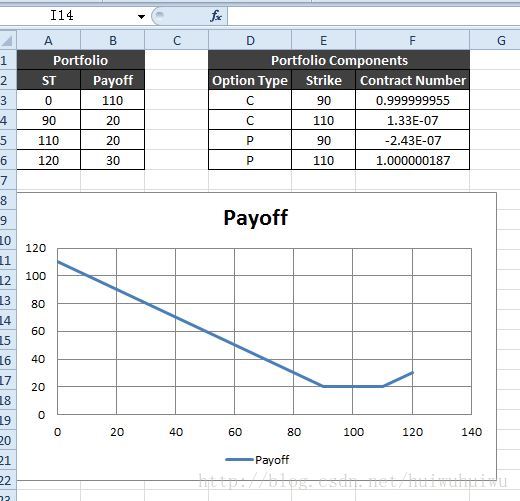
上图左侧的表格就是Input,Payoff图在其下方(strangle);而右侧的表格就是计算得到的结果,我写的这个函数名字为 OpTypeStrikeContractNum 。
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using ExcelDna.Integration;
using FinMktReverseEngineering;
using Excel = Microsoft.Office.Interop.Excel;
using System.Runtime.InteropServices;
using Microsoft.SolverFoundation.Services;
using Microsoft.SolverFoundation.Solvers;
namespace OptionFunctions
{
//Solver Class for calculate the contract number for options
public class CSolver
{
private double[] interpolatedStockPrice;
private double[] interpolatedTargetPayoffs;
private Option[] options;
private int optionNum;
//Constructor
public CSolver(Option[] Options,double[] InterpolatedTargetPayoffs, double[] InterpolatedStockPrice)
{
this.options = Options;
this.interpolatedTargetPayoffs = InterpolatedTargetPayoffs;
this.interpolatedStockPrice = InterpolatedStockPrice;
this.optionNum = options.Length;
}
//Target Function
public double TargetFunction(double[] ContractNum)
{
double sum2OfDiff=0.0;
double sum2OfContractNum=0.0;
double totalPayoff;
for (int i = 0; i < interpolatedStockPrice.Length; i++)
{
totalPayoff = 0.0;
for (int j = 0; j < options.Length; j++)
{
totalPayoff+= options[j].Payoff(interpolatedStockPrice[i]) * ContractNum[j];
sum2OfContractNum += Math.Pow(ContractNum[j]-Math.Round(ContractNum[j],0), 2); //Very important! To avoid trivial answers!!!
}
sum2OfDiff += Math.Pow(interpolatedTargetPayoffs[i] - totalPayoff, 2); //Residuals^2
}
return sum2OfDiff+sum2OfContractNum;
}
//Solver
internal double[] IndidualSolve()
{
var hls = new HybridLocalSearchSolver();
int[] contractNumID = new int[optionNum];
double[] results=new double[optionNum];
//Add variable in the solver
for (int i = 0; i < contractNumID.Length; i++)
{
hls.AddVariable(out contractNumID[i],
Microsoft.SolverFoundation.Common.Rational.NegativeInfinity,
Microsoft.SolverFoundation.Common.Rational.PositiveInfinity,
false);
}
//Solving
hls.AddGoal(hls.CreateNaryFunction(TargetFunction, contractNumID));//目标函数最小化
var hlsr = hls.Solve(new HybridLocalSearchParameters());
//Set results
for (int i = 0; i < results.Length; i++)
{
results[i] = hlsr.GetValue(contractNumID[i]);
}
return results;
}
}
public class OptionFunctions
{
//Function OptionPrice
[ExcelFunction(Description = "Exact solution for European option", Category = "Option Functions")]
public static double OptionPrice([ExcelArgument(Description = @"Call (""C"") or a put (""P"")")]string optionType,
[ExcelArgument(Description = @"Stock")]double underlying, [ExcelArgument(Description = @"Risk-free rate")]double interestRate,
[ExcelArgument(Description = @"Volatility")]double volatility, [ExcelArgument(Description = @"Strike price")]double strikePrice,
[ExcelArgument(Description = @"Time to maturity(in years)")]double timeToMaturity, [ExcelArgument(Description = @"Cost of carry")]double costOfCarry)
{
// Basic validation -
if (underlying <= 0.0 || volatility <= 0.0 || timeToMaturity <= 0.0 || strikePrice <= 0.0)
{
// Exception will be returned to Excel as #VALUE.
throw new ArgumentException();
}
Option o = new Option();
o.otyp = optionType;
o.r = interestRate;
o.sigma = volatility;
o.K = strikePrice;
o.T = timeToMaturity;
o.b = costOfCarry;
return o.Price(underlying);
}
//Function OptionPriceGreeks
[ExcelFunction(Description = "Compute exact solution for a European option, and returns price and greeks as a two-column, "
+ "six-row array with names and values", Category = "Option Functions")]
public static object[,] OptionPriceGreeks([ExcelArgument(Description = @"Call (""C"") or a put (""P"")")]string optionType,
[ExcelArgument(Description = @"Value of the underlying stock")]double underlying, [ExcelArgument(Description = @"Risk-free rate")]double interestRate,
[ExcelArgument(Description = @"Volatility")]double volatility, [ExcelArgument(Description = @"Strike price")]double strikePrice,
[ExcelArgument(Description = @"Time to maturity(years)")]double timeToMaturity, [ExcelArgument(Description = @"Cost of carry")]double costOfCarry)
{
// Basic validation
if (underlying <= 0.0 || volatility <= 0.0 || timeToMaturity <= 0.0 || strikePrice <= 0.0)
{
// Exception will be returned to Excel as #VALUE.
throw new ArgumentException();
}
Option o = new Option();
o.otyp = optionType;
o.r = interestRate;
o.sigma = volatility;
o.K = strikePrice;
o.T = timeToMaturity;
o.b = costOfCarry;
return new object[7, 2]{
{"Price", o.Price(underlying)},
{"Delta", o.Delta(underlying)},
{"Gamma", o.Gamma(underlying)},
{"Vega", o.Vega(underlying)},
{"Theta", o.Theta(underlying)},
{"Rho", o.Rho(underlying)},
{"Coc", o.Coc(underlying)}
};
}
//Function Payoff
[ExcelFunction(Description = "Payoff for European option", Category = "Option Functions")]
public static object[,] Payoff(
[ExcelArgument(Description = @"Call (""C"") or a put (""P"")")]object[] optionType,
[ExcelArgument(Description = @"Strike price")]object[] strikes)
{
int len=optionType.Length;
//Option and Stock Price at T array
<span style="white-space:pre"> </span> Option[] options;
double[] st;
double[] payoffs;
options= new Option[len];
st = new double[len + 2];
payoffs=new double[len+2];
//Initiate the first element st=0.0
st[0] = 0.0;
st[len + 1] = (double)strikes[len⑴]+10.0; //The last ST is last strike +10.0
for (int i = 0; i < len; i++)
<span style="white-space:pre"> </span> {
<span style="white-space:pre"> </span> options[i]=new Option();
options[i].otyp=(string)optionType[i];
options[i].K=(double)strikes[i];
st[i + 1] = (double)strikes[i]; //Set st as strike price
}
//Payoffs at different strockPrice
payoffs = COptionPayoff.OptionPayoff(st, options);
//Return result: St and corresponding Payoff
object[,] result;
result = new object[len+2,2];
for (int i = 0; i < len+2; i++)
<span style="white-space:pre"> </span> {
<span style="white-space:pre"> </span> result[i,0]=(double)st[i];
result[i,1]=(double)payoffs[i];
<span style="white-space:pre"> </span> }
return result;
}
//Return corresponding option contract number by minimizing square of sum of the payoff difference
//ST: 0, 100, 110, 120, 140, 150
//Payoff: 0, 10, 20, 20, 10, 10
[ExcelFunction(Description = "Return corresponding option contract number by minimizing square of sum of the payoff difference ", Category = "Option Functions")]
public static object[,] OpTypeStrikeContractNum(
[ExcelArgument(Description = @"Stock price at maturity")]object[] StockPrices,
[ExcelArgument(Description = @"Target payoffs")]object[] TargetPayoffs)
{
int obsNum = StockPrices.Length; //input number of stock price and target payoffs
int optionNumNeeded = 2*(obsNum - 2); //option number needed
int numAfterInterpolation = obsNum * 2 - 2;
double[] ContractNum; //1st col: Type; 2nd col: Strike; 3rd col: ContractNum
double[] interpolatedStockPrice;
double[] interpolatedTargetPayoffs;
Option[] options;
//Initiate the needed options
options = new Option[optionNumNeeded];
ContractNum = new double[optionNumNeeded];
interpolatedStockPrice = new double[numAfterInterpolation]; //10
interpolatedTargetPayoffs = new double[numAfterInterpolation]; //10
//Set options strike prices
for (int i = 0; i < obsNum⑵; i++) //0,1,2,3
{
//Set the Option Instances
options[i] = new Option();
options[i].otyp = "C";
options[i].K = (double)StockPrices[i + 1];
options[i + optionNumNeeded / 2] = new Option();
options[i + optionNumNeeded / 2].otyp = "P";
options[i + optionNumNeeded / 2].K = (double)StockPrices[i + 1];
//Set certain interpolated stock prices
interpolatedStockPrice[i*2]=(double)StockPrices[i]; //0,2,4,6
interpolatedTargetPayoffs[i*2]=(double)TargetPayoffs[i];
}
//Set the last two elements in the interpolation
interpolatedStockPrice[numAfterInterpolation - 2] = (double)StockPrices[obsNum - 2];
interpolatedStockPrice[numAfterInterpolation - 1] = (double)StockPrices[obsNum - 1];
interpolatedTargetPayoffs[numAfterInterpolation - 2] = (double)TargetPayoffs[obsNum - 2];
interpolatedTargetPayoffs[numAfterInterpolation - 1] = (double)TargetPayoffs[obsNum - 1];
//Interpolation
for (int i = 1; i < optionNumNeeded; i += 2)
{
interpolatedStockPrice[i] = 0.5 * (interpolatedStockPrice[i - 1] + interpolatedStockPrice[i + 1]);
interpolatedTargetPayoffs[i] = 0.5 * (interpolatedTargetPayoffs[i - 1] + interpolatedTargetPayoffs[i + 1]);
}
//Solver
CSolver solver = new CSolver(options, interpolatedTargetPayoffs, interpolatedStockPrice);
ContractNum = solver.IndidualSolve();
//result => 1st column is option type; 2nd column is strike; 3rd column is contract number
object[,] result = new object[optionNumNeeded,3];
for (int i = 0; i < optionNumNeeded; i++)
{
result[i, 0] = (string)options[i].otyp;
result[i, 1] = (double)options[i].K;
result[i,2] =(double) ContractNum[i];
}
return result;
}
}
}
例如,1个Strangle+Put:

------分隔线----------------------------
下一篇 vb学习笔记
------分隔线----------------------------