卡特兰数
Catalan数的定义：
设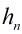
表示用下面的方法把凸多边形区域分成3角形区域的方法数：在有n+1条边的凸多边形区域内通过插入在其中不相交的对角线而把它分成3角形区域。定义
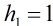。则
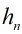满足递推关系
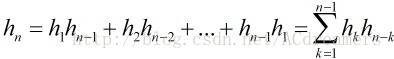
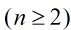
这个递推关系的解是：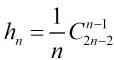
，这里的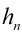
叫做Catalan数。
那末上面的递推式的正确性我们可以简单描写1下便可：
证明：这里由于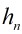
表示依照上述规则划分的3角形区域个数，那末我们随意选1条多边形的1条边作为基边，那末
再在剩余的n⑴个点当选1个点，我们把所选的1条边的两点分别与所选的那1点连接起来，那末多边形被划
分成3部份，1部份有k+1条边，1部份有3条边，另外一部份有n-k+1条边，那末这样就划分成了子问题了，所
以依照这个思路可以证明递推式成立。
那末根据递推式是如何推出Catalan数的通项公式呢？
这里用到了生成函数：我们很容易写出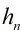
的生成函数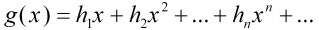
我们进1步计算
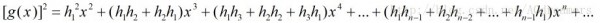
由于有：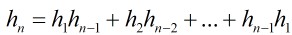
，所以进1步得到：
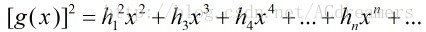，由于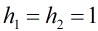
所以有：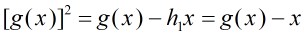
，解之得到：
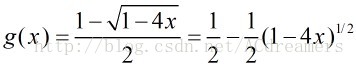，另外一个解不符合，舍去。
那末根据牛顿2项式有：
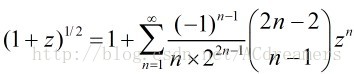
那末带入化简得到：
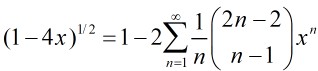
那末我们终究得到：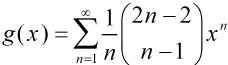
所以：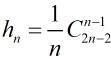
，这就是Catalan的推导进程。
卡特兰数的利用
1、括号化问题
矩阵连乘：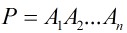
，根据乘法结合律，不改变其顺序，只用括号表示成对的乘积，问有几种括号化的方案？
2、出栈次序问题
1个栈(无穷大)的进栈序列为1,2,3,..n,有多少个不同的出栈序列?
类似问题
a、有2n个人排成1行进入剧院，入场费5元。其中只有n个人有1张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？(将持5元者到达视作将5元入栈，持10元者到达视作使栈中某5元出栈)
b、n个1和n个0组成1个2n位的2进制数，要求从左到右扫描，0的累计数不小于1的累计数，求满足条件的的数。
c、12个人排成两排，每排必须是从矮到高排列，而且第2排比对应的第1排的人高，问排列方式有多少种？
我们先把这12个人从低到高排列,然后,选择6个人排在第1排,那末剩下的6个肯定是在第2排.用0表示对应的人在第1排,用1表示对应的人在第2排,那末含有6个0,6个1的序列,就对应1种方案.
比如000000111111就对应着
第1排：0 1 2 3 4 5
第2排：6 7 8 9 10 11
010101010101就对应着
第1排：0 2 4 6 8 10
第2排：1 3 5 7 9 11问题转换为，这样的满足条件的01序列有多少个。与情况b1样。
3、给定节点组成2叉树的问题
给定N个节点，能构成多少种形状不同的2叉树？
先取1个点作为顶点,然后左侧顺次可以取0至N⑴个相对应的,右侧是N⑴到0个,两两配对相乘,就是h(0)*h(n⑴) + h(2)*h(n⑵) + + h(n⑴)h(0)=h(n))能构成h（N）个
4.n*n棋盘从左下角走到右上角而不穿过主对角线的走法
5.n个+1和n个⑴构成的2n项序列，其部份和总满足：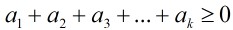
的序列的个数。
Catalan数的高精度处理：利用递归式： h(n)=((4*n⑵)/(n+1))*h(n⑴)