Trie树的详解及应用
栏目:php教程时间:2015-01-21 08:28:39
Trie树,又称单词查找树或键树,是1种树形结构,是1种哈希树的变种。典型利用是用于统计和排序大量的字符串(但不但限于字符串),所以常常被搜索引擎系统用于文本词频统计。它的优点是:最大限度地减少无谓的字符串比较,查询效力比哈希表高。Trie的核心思想是空间换时间。利用字符串的公共前缀来下降查询时间的开消以到达提高效力的目的。
1、插入进程
对1个单词,从根开始,沿着单词的各个字母所对应的树中的节点分支向下走,直到单词遍历完,将最后的节点标记为红色,表示该单词已插入Trie树。
2、查询进程
一样的,从根开始依照单词的字母顺序向下遍历trie树,1旦发现某个节点标记不存在或单词遍历完成而最后的节点未标记为红色,则表示该单词不存在,若最后的节点标记为红色,表示该单词存在。
字典树的数据结构:
利用串构建1个字典树,这个字典树保存了串的公共前缀信息,因此可以下降查询操作的复杂度。
下面以英文单词构建的字典树为例,这棵Trie树中每一个结点包括26个孩子结点,由于总共有26个英文字母(假定单词都是小写字母组成)。
则可声明包括Trie树的结点信息的结构体:
其中next是1个指针数组,寄存着指向各个孩子结点的指针。
如给出字符串"abc","ab","bd","dda",根据该字符串序列构建1棵Trie树。则构建的树以下:
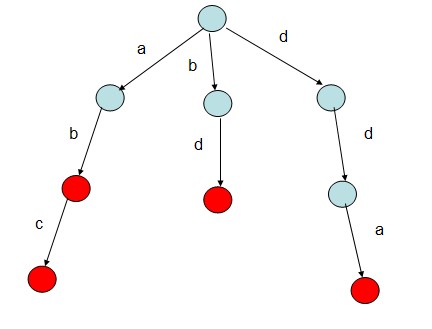
Trie树的根结点不包括任何信息,第1个字符串为"abc",第1个字母为'a',因此根结点中数组next下标为'a'⑼7的值不为NULL,其他同理,构建的Trie树如图所示,红色结点表示在该处可以构成1个单词。很明显,如果要查找单词"abc"是不是存在,查找长度则为O(len),len为要查找的字符串的长度。而若采取1般的逐一匹配查找,则查找长度为O(len*n),n为字符串的个数。明显基于Trie树的查找效力要高很多。
如上图中:Trie树中存在的就是abc、ab、bd、dda4个单词。在实际的问题中可以将标记色彩的标志位改成数量count等其他符合题目要求的变量。
2、 使用hash:我们用hash存下所有字符串的所有的前缀子串。建立存有子串hash的复杂度为O(n*len)。查询的复杂度为O(n)* O(1)= O(n)。
在Trie树中主要有3个操作,插入、查找和删除。1般情况下Trie树中很少存在删除单独某个结点的情况,因此只斟酌删除整棵树。
1、插入
假定存在字符串str,Trie树的根结点为root。i=0,p=root。
1)取str[i],判断p->next[str[i]⑼7]是不是为空,若为空,则建立结点temp,并将p->next[str[i]⑼7]指向temp,然后p指向temp;
若不为空,则p=p->next[str[i]⑼7];
2)i++,继续取str[i],循环1)中的操作,直到遇到结束符'�',此时将当前结点p中的 exist置为true。
2、查找
假定要查找的字符串为str,Trie树的根结点为root,i=0,p=root
1)取str[i],判断判断p->next[str[i]⑼7]是不是为空,若为空,则返回false;若不为空,则p=p->next[str[i]⑼7],继续取字符。
2)重复1)中的操作直到遇到结束符'�',若当前结点p不为空并且 exist 为true,则返回true,否则返回false。
3、删除
Trie树的利用:
Trie 的强大的地方就在于它的时间复杂度。它的插入和查询时间复杂度都为 O(k) ,其中 k 为 key 的长度,与
Trie 中保存了多少个元素无关。Hash 表号称是 O(1) 的,但在计算 hash 的时候就肯定会是 O(k) ,而且还有碰撞之类的问题;Trie 的缺点是空间消耗很高。
Trie树特性:
1)根节点不包括字符,除根节点外每个节点都只包括1个字符。
2)从根节点到某1节点,路径上经过的字符连接起来,为该节点对应的字符串。
3)每一个节点的所有子节点包括的字符都不相同。
4)如果字符的种数为n,则每一个结点的出度为n,这也是空间换时间的体现,浪费了很多的空间。
5)插入查找的复杂度为O(n),n为字符串长度。
1、插入进程
对1个单词,从根开始,沿着单词的各个字母所对应的树中的节点分支向下走,直到单词遍历完,将最后的节点标记为红色,表示该单词已插入Trie树。
2、查询进程
一样的,从根开始依照单词的字母顺序向下遍历trie树,1旦发现某个节点标记不存在或单词遍历完成而最后的节点未标记为红色,则表示该单词不存在,若最后的节点标记为红色,表示该单词存在。
字典树的数据结构:
利用串构建1个字典树,这个字典树保存了串的公共前缀信息,因此可以下降查询操作的复杂度。
下面以英文单词构建的字典树为例,这棵Trie树中每一个结点包括26个孩子结点,由于总共有26个英文字母(假定单词都是小写字母组成)。
则可声明包括Trie树的结点信息的结构体:
- typedef struct Trie_node
- {
- int count; // 统计单词前缀出现的次数
- struct Trie_node* next[26]; // 指向各个子树的指针
- bool exist; // 标记该结点处是不是构成单词
- }TrieNode , *Trie;
如给出字符串"abc","ab","bd","dda",根据该字符串序列构建1棵Trie树。则构建的树以下:

Trie树的根结点不包括任何信息,第1个字符串为"abc",第1个字母为'a',因此根结点中数组next下标为'a'⑼7的值不为NULL,其他同理,构建的Trie树如图所示,红色结点表示在该处可以构成1个单词。很明显,如果要查找单词"abc"是不是存在,查找长度则为O(len),len为要查找的字符串的长度。而若采取1般的逐一匹配查找,则查找长度为O(len*n),n为字符串的个数。明显基于Trie树的查找效力要高很多。
如上图中:Trie树中存在的就是abc、ab、bd、dda4个单词。在实际的问题中可以将标记色彩的标志位改成数量count等其他符合题目要求的变量。
已知n个由小写字母构成的平均长度为10的单词,判断其中是不是存在某个串为另外一个串的前缀子串。
下面对照3种方法:
1、 最容易想到的:即从字符串集中从头往后搜,看每一个字符串是不是为字符串集中某个字符串的前缀,复杂度为O(n^2)。2、 使用hash:我们用hash存下所有字符串的所有的前缀子串。建立存有子串hash的复杂度为O(n*len)。查询的复杂度为O(n)* O(1)= O(n)。
3、 使用Trie:由于当查询如字符串abc是不是为某个字符串的前缀时,明显以b、c、d....等不是以a开头的字符串就不用查找了,这样迅速缩小查找的范围和提高查找的针对性。所以建立Trie的复杂度为O(n*len),而建立+查询在trie中是可以同时履行的,建立的进程也就能够成为查询的进程,hash就不能实现这个功能。所以总的复杂度为O(n*len),实际查询的复杂度只是O(len)。
在Trie树中主要有3个操作,插入、查找和删除。1般情况下Trie树中很少存在删除单独某个结点的情况,因此只斟酌删除整棵树。
1、插入
假定存在字符串str,Trie树的根结点为root。i=0,p=root。
1)取str[i],判断p->next[str[i]⑼7]是不是为空,若为空,则建立结点temp,并将p->next[str[i]⑼7]指向temp,然后p指向temp;
若不为空,则p=p->next[str[i]⑼7];
2)i++,继续取str[i],循环1)中的操作,直到遇到结束符'�',此时将当前结点p中的 exist置为true。
2、查找
假定要查找的字符串为str,Trie树的根结点为root,i=0,p=root
1)取str[i],判断判断p->next[str[i]⑼7]是不是为空,若为空,则返回false;若不为空,则p=p->next[str[i]⑼7],继续取字符。
2)重复1)中的操作直到遇到结束符'�',若当前结点p不为空并且 exist 为true,则返回true,否则返回false。
3、删除
删除可以以递归的情势进行删除。
#include<iostream>
#include<cstring>
using namespace std;
typedef struct Trie_node
{
int count; // 统计单词前缀出现的次数
struct Trie_node* next[26]; // 指向各个子树的指针
bool exist; // 标记该结点处是不是构成单词
}TrieNode , *Trie;
TrieNode* createTrieNode()
{
TrieNode* node = (TrieNode *)malloc(sizeof(TrieNode));
node->count = 0;
node->exist = false;
memset(node->next , 0 , sizeof(node->next)); // 初始化为空指针
return node;
}
void Trie_insert(Trie root, char* word)
{
Trie node = root;
char *p = word;
int id;
while( *p )
{
id = *p - 'a';
if(node->next[id] == NULL)
{
node->next[id] = createTrieNode();
}
node = node->next[id]; // 每插入1步,相当于有1个新串经过,指针向下移动
++p;
node->count += 1; // 这行代码用于统计每一个单词前缀出现的次数(也包括统计每一个单词出现的次数)
}
node->exist = true; // 单词结束的地方标记此处可以构成1个单词
}
int Trie_search(Trie root, char* word)
{
Trie node = root;
char *p = word;
int id;
while( *p )
{
id = *p - 'a';
node = node->next[id];
++p;
if(node == NULL)
return 0;
}
return node->count;
}
int main(void)
{
Trie root = createTrieNode(); // 初始化字典树的根节点
char str[12] ;
bool flag = false;
while(gets(str))
{
if(flag)
printf("%d
",Trie_search(root , str));
else
{
if(strlen(str) != 0)
{
Trie_insert(root , str);
}
else
flag = true;
}
}
return 0;
}
Trie树的利用:
1. 字符串检索,词频统计,搜索引擎的热门查询
事前将已知的1些字符串(字典)的有关信息保存到trie树里,查找另外1些未知字符串是不是出现过或出现频率。
举例:
------分隔线----------------------------
------分隔线----------------------------