数据结构基础(20) --图的存储结构
栏目:php教程时间:2015-01-20 08:25:45
图的结构定义
图是由1个顶点集 V 和1个弧集 E构成的数据结构。
Graph = (V , E )
其中,E = {<v,w>| v,w∈V 且 P(v,w)} <v,w>表示从 v 到 w 的1条弧,并称 v 为弧尾,w 为弧头。谓词 P(v,w) 定义了弧 <v,w>的意义或信息。
由顶点集和边集构成的图称作无向图。
如果”弧”是有方向的,则称由顶点集和弧集构成的图为有向图。
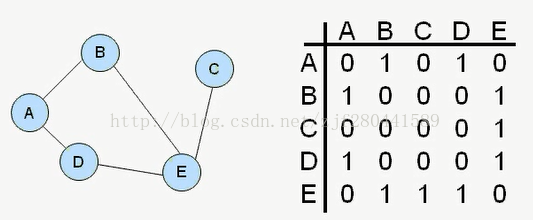
定义:矩阵的元素为
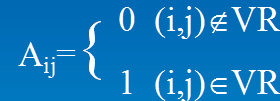
有向图的邻接矩阵为非对称矩阵, 而无向图的邻接矩阵为对称矩阵;
//无向图的邻接矩阵
const int MAX_VERTS = 20;
//顶点
template <typename Type>
class Vertex
{
public:
Vertex(const Type &_node = Type())
: node(_node) {}
private:
Type node;
};
//图
template <typename Type>
class Graph
{
public:
Graph();
~Graph();
void addVertex(const Type &vertex);
void addEdge(int start, int end);
void printMatrix();
private:
Vertex<Type>* vertexList[MAX_VERTS];
int nVerts;
int adjMatrix[MAX_VERTS][MAX_VERTS];
};
template <typename Type>
Graph<Type>::Graph():nVerts(0)
{
for (int i = 0; i < MAX_VERTS; ++i)
for (int j = 0; j < MAX_VERTS; ++j)
adjMatrix[i][j] = 0;
}
template <typename Type>
Graph<Type>::~Graph()
{
for (int i = 0; i < nVerts; ++i)
delete vertexList[i];
}
template <typename Type>
void Graph<Type>::addVertex(const Type &vertex)
{
vertexList[nVerts ++] = new Vertex<Type>(vertex);
}
template <typename Type>
void Graph<Type>::addEdge(int start, int end)
{
//无向图
adjMatrix[start][end] = 1;
adjMatrix[end][start] = 1;
}
template <typename Type>
void Graph<Type>::printMatrix()
{
for (int i = 0; i < nVerts; ++i)
{
for (int j = 0; j < nVerts; ++j)
cout << adjMatrix[i][j] << ' ';
cout << endl;
}
}
//测试代码
int main()
{
Graph<char> g;
g.addVertex('A'); //0
g.addVertex('B'); //1
g.addVertex('C'); //2
g.addVertex('D'); //3
g.addVertex('E'); //4
g.addEdge(0, 1); //A-B
g.addEdge(0, 3); //A-D
g.addEdge(1, 0); //B-A
g.addEdge(1, 4); //B-E
g.addEdge(2, 4); //C-E
g.addEdge(3, 0); //D-A
g.addEdge(3, 4); //D-E
g.addEdge(4, 1); //E-B
g.addEdge(4, 2); //E-C
g.addEdge(4, 3); //E-D
g.printMatrix();
return 0;
}
邻接表
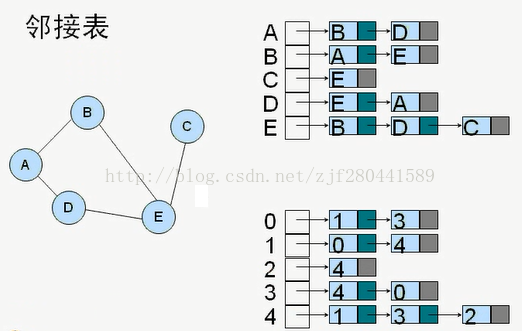
注意:在有向图的邻接表中不容易找到指向该顶点的弧。
//无向图的邻接表
template <typename Type>
class Graph
{
public:
Graph(int _size = 10);
~Graph();
void addVertex(const Type &vertex);
void addEdge(int start, int end);
void printVertex();
void printAdjList();
private:
Type *vertexList;
list<int> *headNode;
int size;
int nVertex;
};
template <typename Type>
Graph<Type>::Graph(int _size):size(_size), nVertex(0)
{
vertexList = new Type[size];
headNode = new list<int>[size];
}
template <typename Type>
Graph<Type>::~Graph()
{
delete []vertexList;
delete []headNode;
}
template <typename Type>
void Graph<Type>::addVertex(const Type &vertex)
{
vertexList[nVertex ++] = vertex;
}
template <typename Type>
void Graph<Type>::addEdge(int start, int end)
{
headNode[start].push_back(end);
}
template <typename Type>
void Graph<Type>::printVertex()
{
cout << vertexList[0];
for (int i = 1; i < nVertex; ++i)
cout << ' ' << vertexList[i];
cout << endl;
}
template <typename Type>
void Graph<Type>::printAdjList()
{
for (int i = 0; i < nVertex; ++i)
{
cout << i;
for (list<int>::iterator iter = headNode[i].begin();
iter != headNode[i].end();
++iter)
cout << " -> " << *iter;
cout << endl;
}
}
//测试代码
int main()
{
Graph<char> g;
g.addVertex('A'); //0
g.addVertex('B'); //1
g.addVertex('C'); //2
g.addVertex('D'); //3
g.addVertex('E'); //4
g.printVertex();
g.addEdge(0, 1); //A-B
g.addEdge(0, 3); //A-D
g.addEdge(1, 0); //B-A
g.addEdge(1, 4); //B-E
g.addEdge(2, 4); //C-E
g.addEdge(3, 0); //D-A
g.addEdge(3, 4); //D-E
g.addEdge(4, 1); //E-B
g.addEdge(4, 2); //E-C
g.addEdge(4, 3); //E-D
g.printAdjList();
return 0;
}
------分隔线----------------------------
------分隔线----------------------------