活动安排问题(贪心算法)
栏目:php教程时间:2014-12-13 08:31:16
问题描写:
有n个活动的活动集合E ,其中每个活动都要求使用同1个资源,而在同1个时刻内资源只能被1个活动使用,每个活动都有开始是时间和结束时间,要求从活动集合E当选出m个活动,使着m个活动都能顺利进行,即也就是每一个活动的活动时间都相互不交叉,求m的最大值和 被选中的活动序号。
例如输入:
活动编号 活动开始时间 活动结束时间
1 1 4
2 3 5
3 0 6
4 5 7
5 3 8
6 5 9
7 6 10
8 8 11
9 8 12
10 2 13
11 12 14
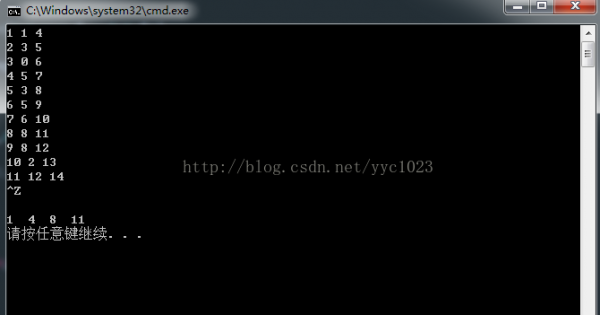
本程序利用贪心算法解决,输出的答案是:
应当选择的活动编号为:
1 4 8 11(即最大可以安排这4个活动)
#include<iostream>
#include<iterator>
#include<vector>
#include<algorithm>
using namespace std;
/*
*活动安排问题(贪心算法)
*/
struct Act
{
int beg;//活动的开始时间
int end;//活动的结束时间
int index;//活动的编号
friend ostream & operator<<(ostream &o,const Act &A);
friend istream & operator>>(istream &o, Act &A);
};
ostream & operator<<(ostream &o,const Act &A)
{
o<<A.beg<<"---"<<A.end<<" ";
return o;
}
istream & operator>>(istream &o, Act &A)
{
o>>A.index>>A.beg>>A.end;
return o;
}
bool cmp(Act & act1,Act & act2)
{
if(act1.end<act2.end)
{
return true;
}else
{
return false;
}
}
vector<int> GreedySelector(vector<Act> & acts)
{
//首先把活动依照活动的结束时间进行排序
sort(acts.begin(),acts.end(),cmp);
//在排序后的活动集合当选择可行的活动
vector<int> res;
res.push_back(acts[0].index);//首先选中第1个活动
int now = 0;//当前选中的活动下标
for (int i = 1; i < acts.size(); i++)
{
if(acts[i].beg>=acts[now].end)
{
now = i;
res.push_back(acts[i].index);
}
}
return res;
}
int main()
{
vector<Act> acts;//可选活动集
copy(istream_iterator<Act>(cin),istream_iterator<Act>(),back_inserter(acts));
cout<<endl;
vector<int> res_act;//得出的方案中的活动编号集
res_act = GreedySelector(acts);
//输出结果
copy(res_act.begin(),res_act.end(),ostream_iterator<int>(cout," "));
cout<<endl;
}
------分隔线----------------------------
------分隔线----------------------------