Spark MLlib NaiveBayes 贝叶斯分类器
1.1朴素贝叶斯公式
贝叶斯定理:

其中A为事件,B为种别,P(B|A)为事件A条件下属于B种别的几率。
朴素贝叶斯分类的正式定义以下:
1、设 为1个待分类项,而每一个a为x的1个特点属性。
为1个待分类项,而每一个a为x的1个特点属性。
2、有种别集合 。
。
3、计算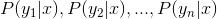 。
。
4、如果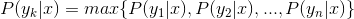 ,则
,则 。
。
那末现在的关键就是如何计算第3步中的各个条件几率:
1、找到1个已知分类的待分类项集合,这个集合叫做训练样本集。
2、统计得到在各种别下各个特点属性的条件几率估计。即  。
。
3、如果各个特点属性是条件独立的,则根据贝叶斯定理有以下推导:

由于分母对所有种别为常数,由于我们只要将份子最大化皆可。又由于各特点属性是条件独立的,所以有:

1.2 NaiveBayesModel源码解析
1、NaiveBayesModel主要的3个变量:
1)labels:种别
scala> labels
res56: Array[Double] = Array(2.0, 0.0, 1.0)
2)pi:各个label的先验几率
scala> pi
res57: Array[Double] = Array(⑴.1631508098056809, -0.9808292530117262, ⑴.1631508098056809)
3)theta:存储各个特点在各个种别中的条件几率。
scala> theta
res58: Array[Array[Double]] = Array(Array(⑵.032921526044943, ⑴.8658674413817768, -0.33647223662121295), Array(-0.2451224580329847, ⑵.179982770901713, ⑵.26002547857525), Array(⑴.9676501356917193, -0.28410425110389714, ⑵.2300144001592104))
4)lambda:平滑因子
2、NaiveBayesModel代码
1) train
/**
* Run the algorithm with the configured parameters on an input RDD of LabeledPoint entries.
*
* @param data RDD of [[org.apache.spark.mllib.regression.LabeledPoint]].
*/
def run(data: RDD[LabeledPoint]) = {
// requireNonnegativeValues:取每个样本数据的特点值,以向量情势存储,特点植必须为非负数。
val requireNonnegativeValues: Vector => Unit = (v: Vector) => {
val values = vmatch {
case SparseVector(size, indices, values) =>
values
case DenseVector(values) =>
values
}
if (!values.forall(_ >=0.0)) {
thrownew SparkException(s"Naive Bayes requires nonnegative feature values but found $v.")
}
}
// Aggregates term frequencies per label.
// TODO: Calling combineByKey and collect creates two stages, we can implement something
// TODO: similar to reduceByKeyLocally to save one stage.
// aggregated:对所有样本数据进行聚合,以label为key,聚合同1个label的features;
// createCombiner:完成样本从V到C的combine转换,(v: Vector)