程序员人生网站导航

[Java 8] Lambda表达式对递归的优化(下) - 使用备忘录模式(Memoization Pattern)

栏目：互联网时间：2014-11-17 08:24:43

使用备忘录模式(Memoization Pattern)提高性能

这个模式说白了，就是将需要进行大量计算的结果缓存起来，然后在下次需要的时候直接获得就行了。因此，底层只需要使用1个Map就够了。

但是需要注意的是，只有1组参数对应得到的是同1个值时，该模式才有用武之地。

在很多算法中，典型的比如分治法，动态计划(Dynamic Programming)等算法中，这个模式应用的10分广泛。以动态计划来讲，动态计划在求最优解的进程中，会将原有任务分解成若干个子任务，而这些子任务必将还会将本身分解成更小的任务。因此，从整体而言会有相当多的重复的小任务需要被求解。明显，当输入的参数相同时，1个任务只需要被求解1次就行了，求解以后将结果保存起来。待下次需要求解这个任务时，会首先查询这个任务是不是已被解决了，如果答案是肯定的，那末只需要直接返回结果就好了。

就是这么1个简单的优化措施，常常能够将代码的时间复杂度从指数级的变成线性级。

以1个经典的杆切割问题(Rod Cutting Problem)(或这里也有更加正式的定义：维基百科)为例，来讨论1下如何结合Lambda表达式来实现备忘录模式。

首先，简单交代1下这个问题的背景。

1个公司会批发1些杆(Rod)，然后对它们进行零售。但是随着杆的长度不同，能够卖出的价格也是不同的。所以该公司为了将利润最大化，需要结合长度价格信息来决定应当将杆切割成甚么长度，才能实现利润最大化。

比如，下面的代码：

final List<Integer> priceValues = Arrays.asList(2, 1, 1, 2, 2, 2, 1, 8, 9, 15);

表达的意思是：长度为1的杆能够卖2元，长度为2的杆能够卖1元，以此类推，长度为10的杆能够卖15元。

当需要被切割的杆长度为5时，存在的切割方法多达16种(2^(5 - 1))。以下所示：

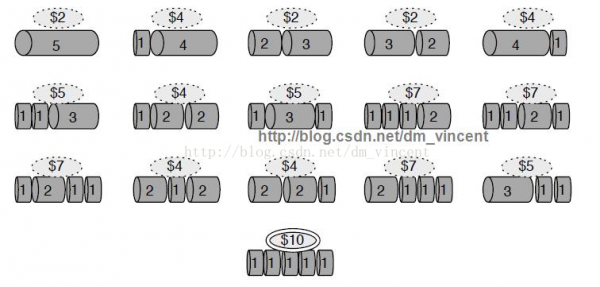
针对这个问题，在不斟酌使用备忘录模式的情况下，可使用动态计划算法实现以下：

public int maxProfit(final int length) {
    int profit = (length <= prices.size()) ? prices.get(length - 1) : 0;
    for(int i = 1; i < length; i++) {
        int priceWhenCut = maxProfit(i) + maxProfit(length - i);
        if(profit < priceWhenCut) profit = priceWhenCut;
    }
    return profit;
}

而从上面的程序可以发现，有很多重复的子问题。对这些重复的子问题进行不断纠结，损失了很多没必要要的性能。分别取杆长为5和22时，得到的运行时间分别为：0.001秒和34.612秒。可见当杆的长度增加时，性能的降落时非常非常显著的。

由于备忘录模式的原理10分简单，因此实现起来也很简单，只需要在以上maxProfit方法的头部加上Map的读取操作并判断结果就能够了。但是这样做的话，代码的复用性会不太好。每一个需要使用备忘录模式的地方，都需要单独写判断逻辑，那末有无1种通用的办法呢？答案是肯定的，通过借助Lambda表达式的气力可以轻易办到，以下代码我们假定有1个静态方法callMemoized用来通过传入1个策略和输入值，来求出最优解：

public int maxProfit(final int rodLenth) {
    return callMemoized(
        (final Function<Integer, Integer> func, final Integer length) -> {
        int profit = (length <= prices.size()) ? prices.get(length - 1) : 0;
        for(int i = 1; i < length; i++) {
            int priceWhenCut = func.apply(i) + func.apply(length - i);
            if(profit < priceWhenCut) profit = priceWhenCut;
        }
        return profit;
        }, rodLenth);
}

让我们仔细分析1下这段代码的意图。首先callMemoized方法接受的参数类型是这样的：

public static <T, R> R callMemoized(final BiFunction<Function<T,R>, T, R> function, final T input)

BiFunction类型的参数function实际上封装了1个策略，其中有3个部份：

Function：通过传入参数T，来得到解答R。这1点从代码int priceWhenCut = func.apply(i) + func.apply(length - i)很明显的就可以够看出来。可以把它想象成1个备忘录的入口。
T：代表求解问题时需要的参数T。
R：代表问题的答案R。

以上的T和R都是指的类型。

下面我们看看callMemoized方法的实现：

public class Memoizer {
    public static <T, R> R callMemoized(final BiFunction<Function<T,R>, T, R> function, final T input) {
        Function<T, R> memoized = new Function<T, R>() {
            private final Map<T, R> store = new HashMap<>();
            public R apply(final T input) {
                return store.computeIfAbsent(input, key -> function.apply(this, key));
            }
        };

        return memoized.apply(input);
    }
}

在该方法中，首先声明了1个匿名Function函数接口的实现。其中定义了备忘录模式的核心---Map结构。然后在它的apply方法中，会借助Java 8中为Map接口新添加的1个computeIfAbsent方法来完成下面的逻辑：

通过传入的key检查(在以上代码中是input)对应的值是不是存在于备忘录的底层Map中
如果存在，跳转到步骤4
如果不存在，根据computeIfAbsent的第2个参数(是1个Lambda表达式)来计算得到key对应的value
返回得到的value

具体到该方法的源码：

default V computeIfAbsent(K key, Function<? super K, ? extends V> mappingFunction) {
    Objects.requireNonNull(mappingFunction);
    V v;
    if ((v = get(key)) == null) {
        V newValue;
        if ((newValue = mappingFunction.apply(key)) != null) {
            put(key, newValue);
            return newValue;
        }
    }

    return v;
}

也能够很清晰地看出以上的几个步骤是如何体现在代码中的。

关键的地方就在于第3步，如果不存在对应的value，那末需要调用传入的Lambda表达式进行求解。以上代码传入的是key -> function.apply(this, key)，这里的this使用的10分奇妙，它实际上指向的就是这个用于容纳Map结构的匿名Function实例。它作为第1个参数传入到算法策略中，同时需要求解的key被当作第2个参数传入到算法策略。这里所谓的算法策略，实际上就是在调用callMemoized方法时，传入的情势为BiFunction<Function<T,R>, T, R>的参数。

因此，所有的子问题仅仅会被求解1次。在得到子问题的答案以后，答案会被放到Map数据结构中，以便将来的使用。这就是借助Lambda表示实现备忘录模式的方法。

以上的代码可能会显得有些奇异，这很正常。在你反复浏览它们后，并且经过自己的思考能够重写它们时，也就是你对Lambda表达式具有更深理解之时。

使用备忘录模式后，杆长依然取5和22时，得到的运行时间分别为：0.050秒和0.092秒。可见当杆的长度增加时，性能并没有如之前那样降落的很利害。这完全是得益于备忘录模式，此时所有的任务都只会被运行1次。

------分隔线----------------------------

上一篇 POJ2029――Get Many Persimmon Trees

下一篇 Android开发之RadioButton单选按钮的使用

------分隔线----------------------------