一种快速开平方并取倒数算法
栏目:互联网时间:2014-11-15 06:44:43
今天在查资料进程中,无意中看到这样1段奇异的代码,决定转载到自己的csdn博客,但是找了半天,愣是没找到csdn转载功能,此前常常看到他人转载文章,然后心里1直在想,是否是转载是1个隐藏功能,或使用甚么命令就能够了。因而特地谷歌了下,原来csdn的转载功能,根本没有甚么快速转载、1键转载,只有对着原文复制、粘贴,然后在自己的博客里面重新排版,最后在发布文章时选择转载,这样该文章就成为1篇转摘的文章了。这么设计也有道理,只有不嫌麻烦的人,才会耐心的完成转载,算是提高了转载的门坎,避免出现大量重复文章。不过,这么设计的副作用就是,浪费了很多时间和精力。吐槽就到这里,还是看看这段奇异的快速开平方并取倒数代码:
float InvSqrt(float x )
{
float xhalf = 0.5f * x;
int i = *( int *)& x;
i = 0x5f3759df - ( i>>1);
x = *( float *)& i;
x = x * (1.5f - xhalf * x * x);
return x;
}
关于该段代码的更多说明,请参看这篇文章《0x5f3759df的数学原理》。 下面为我编写的简单测试代码:
#include "stdafx.h"
#include <stdio.h>
#include <stdlib.h>
#include <windows.h>
#include <math.h>
// 开平方取倒数
float InvSqrt(float x )
{
float xhalf = 0.5f * x;
int i = *( int *)& x;
i = 0x5f3759df - ( i>>1);
x = *( float *)& i;
x = x * (1.5f - xhalf * x * x);
return x;
}
int main()
{
// 比较精度
float val = 0.0f;
val = 1.0f;
printf("计算精度比较:
");
printf("输入值: %f 快速算法: %f VC函数: %f
", val, InvSqrt(val), 1.0f / sqrt(val));
val = 16.0f;
printf("输入值: %f 快速算法: %f VC函数: %f
", val, InvSqrt(val), 1.0f / sqrt(val));
val = 25.0f;
printf("输入值: %f 快速算法: %f VC函数: %f
", val, InvSqrt(val), 1.0f / sqrt(val));
val = 100.0f;
printf("输入值: %f 快速算法: %f VC函数: %f
", val, InvSqrt(val), 1.0f / sqrt(val));
printf("
计算性能比较:
");
int count = 1000000;
DWORD timeStart = 0, timeEnd = 0;
timeStart = GetTickCount();
for (int i = 0; i < count; i++)
{
val = InvSqrt(100.0f);
}
timeEnd = GetTickCount();
printf("快速算法耗时: %f
", (timeEnd - timeStart) * 0.001);
timeStart = GetTickCount();
for (int i = 0; i < count; i++)
{
val = 1.0f / sqrt(100.0f);
}
timeEnd = GetTickCount();
printf("VC函数耗时: %f
", (timeEnd - timeStart) * 0.001);
printf("
");
system("pause");
return 0;
}
这里与sqrt()分别比较了计算精度及计算性能,测试环境为vs2005,普通pc笔记本(实际上是1台年久的、玩的了游戏、写得了代码的小黑)。从对照结果看,该快速算法在计算结果上有1点点误差,但是计算性能上很可观。下图为对照结果: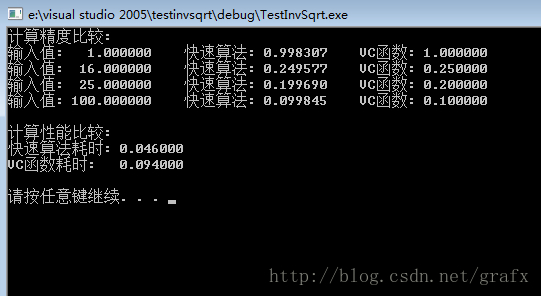
------分隔线----------------------------
------分隔线----------------------------