评分卡模型剖析之一（woe、IV、ROC、信息熵）

信用评分卡模型在国外是一种成熟的预测方法，尤其在信用风险评估以及金融风险控制领域更是得到了比较广泛的使用，其原理是将模型变量WOE编码方式离散化之后运用logistic回归模型进行的一种二分类变量的广义线性模型。

       本文重点介绍模型变量WOE以及IV原理，为表述方便，本文将模型目标标量为1记为违约用户，对于目标变量为0记为正常用户；则WOE(weight of Evidence)其实就是自变量取某个值的时候对违约比例的一种影响，怎么理解这句话呢？我下面通过一个图标来进行说明。

Woe公式如下：

    表中以age年龄为某个自变量，由于年龄是连续型自变量，需要对其进行离散化处理，假设离散化分为5组（至于如何分组，会在以后专题中解释），#bad和#good表示在这五组中违约用户和正常用户的数量分布，最后一列是woe值的计算，通过后面变化之后的公式可以看出，woe反映的是在自变量每个分组下违约用户对正常用户占比和总体中违约用户对正常用户占比之间的差异；从而可以直观的认为woe蕴含了自变量取值对于目标变量（违约概率）的影响。再加上woe计算形式与logistic回归中目标变量的logistic转换(logist_p=ln(p/1-p))如此相似，因而可以将自变量woe值替代原先的自变量值；

讲完WOE下面来说一下IV：

IV公式如下：

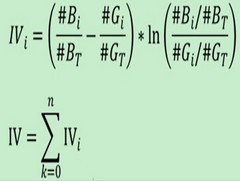
其实IV衡量的是某一个变量的信息量，从公式来看的话，相当于是自变量woe值的一个加权求和，其值的大小决定了自变量对于目标变量的影响程度；从另一个角度来看的话，IV公式与信息熵的公式极其相似。

事实上，为了理解WOE的意义，需要考虑对评分模型效果的评价。因为我们在建模时对模型自变量的所有处理工作，本质上都是为了提升模型的效果。在之前的一些学习中，我也总结了这种二分类模型效果的评价方法，尤其是其中的ROC曲线。为了描述WOE的意义，还真的需要从ROC说起。仍旧是先画个表格。

数据来自于著名的German credit dataset，取了其中一个自变量来说明问题。第一列是自变量的取值，N表示对应每个取值的样本数，n1和n0分别表示了违约样本数与正常样本数，p1和p0分别表示了违约样本与正常样本占各自总体的比例，cump1和cump0分别表示了p1和p0的累计和，woe是对应自变量每个取值的WOE（ln(p1/p0)），iv是woe*(p1-p0)。对iv求和(可以看成是对WOE的加权求和)，就得到IV(information value信息值)，是衡量自变量对目标变量影响的指标之一(类似于gini,entropy那些)，此处是0.666，貌似有点太大了，