hdu 5047 Sawtooth
栏目:互联网时间:2014-09-29 21:26:28
Sawtooth
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)Total Submission(s): 258 Accepted Submission(s): 78
Problem Description
Think about a plane:
● One straight line can divide a plane into two regions.
● Two lines can divide a plane into at most four regions.
● Three lines can divide a plane into at most seven regions.
● And so on...
Now we have some figure constructed with two parallel rays in the same direction, joined by two straight segments. It looks like a character “M”. You are given N such “M”s. What is the maximum number of regions that these “M”s can divide a plane ?
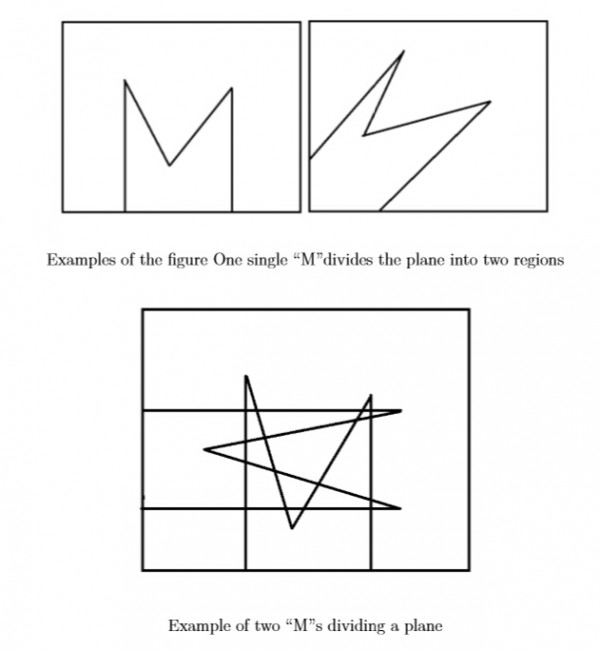
● One straight line can divide a plane into two regions.
● Two lines can divide a plane into at most four regions.
● Three lines can divide a plane into at most seven regions.
● And so on...
Now we have some figure constructed with two parallel rays in the same direction, joined by two straight segments. It looks like a character “M”. You are given N such “M”s. What is the maximum number of regions that these “M”s can divide a plane ?

Input
The first line of the input is T (1 ≤ T ≤ 100000), which stands for the number of test cases you need to solve.
Each case contains one single non-negative integer, indicating number of “M”s. (0 ≤ N ≤ 1012)
Each case contains one single non-negative integer, indicating number of “M”s. (0 ≤ N ≤ 1012)
Output
For each test case, print a line “Case #t: ”(without quotes, t means the index of the test case) at the beginning. Then an integer that is the maximum number of regions N the “M” figures can divide.
Sample Input
2
1
2
Sample Output
Case #1: 2
Case #2: 19
Source
2014 ACM/ICPC Asia Regional Shanghai Online
题解及代码:
推导公式很简单:首先通过看图,我们可以知道,任意两个M都能相交出现16个交点,然后对M进行标号1--n,总的交点数就是∑16*i (1=<i<n),
然后根据:边数+点数+1=分成的区域数,可以算出公式是:8*n^2-7*n+1。因为数比较大,所以会想到用java,结果kuangbin大神卡的很紧Orz....
那就用c++的大数模版来吧,通过观察我们发现:上述公式可以转换一下成n*(8*n-7)+1,这里8*n可以用位运算来算,我们让m=8*n-7,m最大也到
不了10^13,而n最大是10^12,这样我们可以利用大数的思想,将m分成两部分,分别与n进行相乘,最后简单处理一下输出就行了。
Time:187ms
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const ll mod=1000000;
int main()
{
ll n,m,l_m,r_m;
int cas;
scanf("%d",&cas);
for(int ca=1; ca<=cas; ca++)
{
scanf("%I64d",&n);
//printf("%I64d
",8*n*n-7*n+1);
m=(n<<3)-7;
l_m=m/mod;
r_m=m%mod;
l_m*=n;
r_m=r_m*n+1;
l_m=l_m+r_m/mod;
r_m%=mod;
printf("Case #%d: ",ca);
if(l_m) printf("%I64d%06I64d
",l_m,r_m);
else printf("%I64d
",r_m);
}
return 0;
}
------分隔线----------------------------
------分隔线----------------------------